Расчёт деформируемых стержневых систем методом перемещений: Методические указания к индивидуальному расчётному заданию по курсу «Строительная механика», страница 12

       R_iZ – реакция i - й связи в ОСМП от смещений узлов Z₁ , …, Z_n .

         Также по принципу независимости воздействий  суммарная

реакция R_iZ  ( от всех Z одновременно ) представляется как сумма

составляющих от каждого компонента Z  в отдельности:

                                                                     ,                              ( 1.12 )

где – реакция i - й связи от смещения Z_kk - й связи;

                      r_ik– реакция i - й связи от  единичного смещения k - й

                             связи ( от Z_k = 1 ).

1.4.2. Варианты записи и смысл канонических уравнений МП

         Подстановка (1.11) и (1.12) в (1.10) дает систему уравнений

 

                                                                                 ,                  ( 1.13 ) 

называемых  каноническимиуравнениями  метода  перемещений ( КУМП ).

         Это неоднородные алгебраические уравнения, линейные относительно основных неизвестных Z.

         В развёрнутом виде:

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

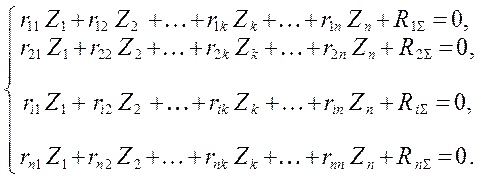            ( 1.14 )

20

Смысл КУМП и их компонентов

          1. Система канонических уравнений в целом по сути –  статические условия эквивалентности основной системы МП  и заданной системы  при одинаковых воздействиях  и  истинных

перемещениях Zрасчётных узлов; по форме – отрицание полных

реакций всех дополнительных связей в расчётных узлах.

20

         2. Произвольное ( i - е ) уравнение – отрицаниеполнойреакции i - йвведённой связи  в  ОСМП  ( суммарной реакции R_i  от заданных  воздействий  ( S )   и   одновременных   смещений   всех введённых связей, равных истинным перемещениям Zрасчётных узлов ).

         3. Левая часть i - го уравнения – полная реакция i - й введённой  связи  в  ОСМП  ( суммарная реакция R_i  от заданных воздействий ( S )  и  одновременных  смещений  всех введённых связей, равных истинным перемещениям Zрасчётных узлов ).

         4. Свободный член i - го уравнения R_iS  – реакция i - йвведён-ной связи в ОСМП от заданных воздействий ( S ).

         5. Слагаемое r_ik Z_k i - го уравнения – реакция R_ik i - йвведён-ной связи  в ОСМП  от смещения k - йсвязи,равного истинному перемещению Z_k .

22

         6. Коэффициент r_ik  принеизвестном Z_k в i - м  уравнении – реакция i - й введенной связи в ОСМП  от  единичного  смещения  k - й  связи  Z_k = 1 ( единичная реакция ).

         Собственные единичные реакции r₁₁, r₂₂ , …, r_ii , …, r_nn введённых связей в ОСМП называются главными коэффициентами канонических уравнений МП, а величины – побочными  реакциями (побочными коэффициентами уравнений).

         По теореме Рэлея о взаимности единичных реакций r_ik = r_ki .

19

         Матричная форма записи канонических уравнений ( 1.13 ) и ( 1.14 ):

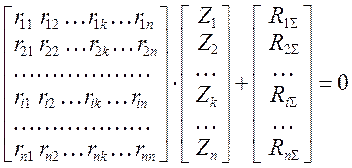   или    ( 1.15 )

                rZR_S

21

         В ( 1.15 ):

r – матрица коэффициентов КУМП  – матрица внешней  жёст-

       кости  основной  системы МП  по  направлениям  основных

       неизвестных Z ;

Z – матрица  ( при одном варианте  заданных воздействий  –  век-

       тор ) основных неизвестных – независимых угловых и линей-

       ных перемещений расчётных узлов;

R_S – матрица ( при одном варианте заданных воздействий  –  век-

       тор )  реакций дополнительных связей  в расчётных узлах  от

       заданных воздействий.