Расчёт деформируемых стержневых систем методом перемещений: Методические указания к индивидуальному расчётному заданию по курсу «Строительная механика», страница 18

Примечания:  1). Для элемента  типа 4  эпюры М и Q  от поперечных нагрузок – как в однопролётной балке, шарнирно опёртой по концам.

                        2). При вычислении изгибающих моментов  в  концевых сечениях элемента  по приведённым в таблице формулам  в случае загружения

                             сосредоточенным моментом М может получиться отрицательное число. Это означает, что ордината эпюры М должна быть отложена

                             от оси эпюры в противоположную сторону по сравнению с изображённой на схеме в таблице.

1.5. Определение основных неизвестных, вычисление усилий

в заданной системе и проверки результатов расчёта

39

          Решением системы канонических уравнений находятся основные неизвестные  Z₁ , Z₂ , …, Z_n ,  используемые  затем  для вычисления усилий S в ОСМП от этих смещений расчётных   узлов вместе с заданными воздействиями. Если перемещения        Z₁ , Z₂ , …, Z_n  найдены правильно,  то усилия в ОСМП могут считаться равными  ( с  допустимыми  вычислительными  погрешностями )  искомым  усилиям  в  заданной рассчитываемой системе. Согласно принципу суперпозиции воздействий,

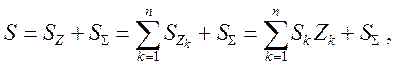                            ( 1.26 )

где S_k – усилия в k - м единичном состоянии ОСМП ( от Z_k = 1 );

      S_S – усилия в ОСМП от заданных воздействий.

          Для элементов с преобладающим изгибом усилия S – это изгибающие моменты M и поперечные силы Q, для элементов типа затяжек, подкосов и т.п., а также для стержней ферм S – это продольные силы N. При выполнении расчёта «вручную» в первую очередь вычисляются изгибающие моменты   

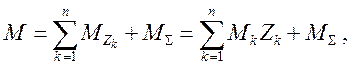                                 ( 1.27 )

затем – поперечные силы ( с помощью дифференциальной зависимости  Q = dM / dx  и  условий  равновесия  отдельных  элементов ),  после чего из уравнений равновесия узлов находятся продольные силы N.

          При необходимости, кроме силовых факторов в рассчитываемой системе, могут быть найдены и перемещения сечений любого элемента – для этого по найденным значениям перемещений Z  расчётных узлов определяются  компоненты смещений его концевых сечений, а затем одним из известных методов – Максвелла – Мора  или  начальных параметров – искомые перемещения сечений. Особенно просто эта задача решается для элемента постоянного сечения, уравнение изогнутой оси которого при равномерной нагрузке по всей длине есть полином четвёртой степени, а при отсутствии нагрузки – третьей степени.

          Результаты расчёта, особенно выполненного «вручную», требуют проверки ввиду достаточно большого числа причин, по которым возможно возникновение ошибок на разных этапах решения задачи – к ним, кроме сугубо арифметических, можно отнести и неправильную номинацию типов элементов ОСМП,   и нарушения условий совместности деформаций элементов        в единичных состояниях ОСМП, и неверное использование стандартных ( табличных )  данных,  и  несоответствие ( в частности, по знакам ) усилий в элементах их деформациям, и др. Часть ошибок, особенно возникших на стадии решения системы КУМП и в последующих процедурах, не выявляются вышеописанными промежуточными проверками  ( например, подстановка неверного значения нагрузки в табличную формулу ).

52

50

          Полная проверка результатов расчёта деформируемой системы методом перемещений состоит из двух частей:

          1) статическая проверка, заключающаяся в том, что при найденных значениях силовых факторов и заданных нагрузках выполняется контроль выполнения условий равновесия 

               а) узлов,

               б) произвольно выделенных частей системы,

53

               в) системы в целом;

51

          2) кинематическая ( деформационная ) проверка – вычисление перемещений, которые в заданной системе заведомо равны нулю ( по направлениям жёстких связей ).