
своими концами, он может рассматриваться

как жёсткая линейная связь между этими
узлами.
*) Другой путь – использование
элементов с присоединёнными к ним концевыми упругими связями; в этом случае для
узла на рис. 1.4 будет nж.у. = 2.
Из-за этого некоторые перемещения узлов перестают быть независимыми, и степень
линейной подвижности узлов уменьшается. С учётом допущения ( 1.4
) она находится как

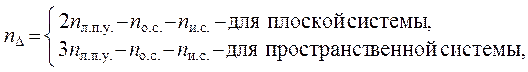
(
1.5
)
где nи.с. – количество
изгибаемых стержней системы.
Формулы ( 1.5 ) в
некоторых особых случаях могут давать неверный результат – объяснение будет
приведено ниже.


Ещё одно следствие условия (
1.4
): взаимное (
относительное
) линейное перемещение D
be концов
стержня при деформации можно считать происходящим по нормали к его
продольной оси (
рис. 1.6, а
); при этом если один из
концов деформируемого стержня неподвижен, то истинная траектория движения его
противоположного конца (
кривая
ее* на рис. 1.6, б
) заменяется касательной к ней – прямой
ее’, перпендикулярной к исходной оси
be.

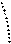

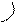


 а)
б)
а)
б)
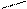
Рис.
1.6

Следует иметь в виду, что если для систем с
небольшим числом элементов применение вышеизложенной рабочей гипотезы не вносит
заметных погрешностей в результат расчёта в сравнении с точными значениями
усилий и перемещений, то для сложных сооружений типа многоэтажных многопролётных
рам ошибки, возникающие из-за
пренебрежения продольными деформациями стержней,
могут получаться
недопустимо большими.
Важно:
учёт сдвига для изгибаемых стержней или пренебрежение этим видом
деформации не влияет на число основных неизвестных перемещений ( степень
кинематической неопределимости системы ).
В простых системах, особенно
с ортогональным расположением стержней, выявление независимых линейных перемещений
узлов, принимаемых за основные неизвестные, возможно непосредственной оценкой
предполагаемых деформаций системы. Например, в раме с вертикальными стойками
( рис. 1.7 ) перемещения пяти узлов могут считаться горизонтальными ( на основании свойства, проиллюстрированного рис. 1.6, б ). При
этом обнаруживается равенство перемещений: uA=uB=uC и uD=uH . Следовательно, за основные
неизвестные должны быть приняты два из пяти перемещений – по одному из каждой
группы одинаковых величин, например, uA и uD , т.е. nD = 2.






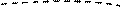
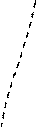
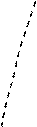




 Рис. 1.7
Рис. 1.7
По формуле ( 1.5 ): nD = 2nл.п.у. – nо.с.– nи.с. = 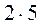 – 0 – 8 = 2.
– 0 – 8 = 2.

 Характеристику nD можно определять как минимальное число линейных
связей, которые необходимо наложить на расчётные узлы, чтобы сделать их
линейно неподвижными.
Характеристику nD можно определять как минимальное число линейных
связей, которые необходимо наложить на расчётные узлы, чтобы сделать их
линейно неподвижными.
Так, если узлы
А и
D рамы
(
рис. 1.7
) закрепить горизонтальными
*) линейными
связями (
по одной в каждом узле –
![]()
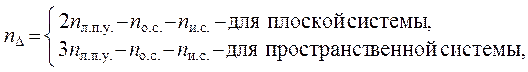 ( 1.5 )
( 1.5 )

![]()
![]()

![]()
![]()
![]()
 а)
б)
а)
б)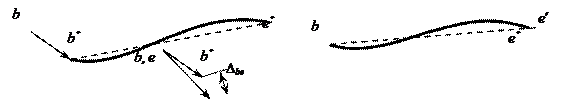
 Следует иметь в виду, что если для систем с
небольшим числом элементов применение вышеизложенной рабочей гипотезы не вносит
заметных погрешностей в результат расчёта в сравнении с точными значениями
усилий и перемещений, то для сложных сооружений типа многоэтажных многопролётных
рам ошибки, возникающие из-за пренебрежения продольными деформациями стержней,
могут получаться недопустимо большими.
Следует иметь в виду, что если для систем с
небольшим числом элементов применение вышеизложенной рабочей гипотезы не вносит
заметных погрешностей в результат расчёта в сравнении с точными значениями
усилий и перемещений, то для сложных сооружений типа многоэтажных многопролётных
рам ошибки, возникающие из-за пренебрежения продольными деформациями стержней,
могут получаться недопустимо большими.
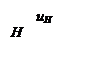
![]()


![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() Рис. 1.7
Рис. 1.7![]() – 0 – 8 = 2.
– 0 – 8 = 2.![]()
![]() Характеристику nD можно определять как минимальное число линейных
связей, которые необходимо наложить на расчётные узлы, чтобы сделать их
линейно неподвижными.
Характеристику nD можно определять как минимальное число линейных
связей, которые необходимо наложить на расчётные узлы, чтобы сделать их
линейно неподвижными.