Расчёт деформируемых стержневых систем методом перемещений: Методические указания к индивидуальному расчётному заданию по курсу «Строительная механика», страница 4

         В  отличие  от  степени  статической  неопределимости  n_st , однозначно равной числу лишних связей в статически неопределимой системе, степень кинематической неопределимости не является величиной, зависящей только от свойств рассчитываемой системы, – она зависит от того, как назначены расчётные узлы ( согласно п. 4 на стр. 4, их число может задаваться по усмотрению расчётчика ), а также от принимаемых рабочих гипотез ( будут рассмотрены ниже ) и особенностей элементов, используемых  в  качестве типовых ( элементы могут быть простыми или достаточно сложными, с собственными внутренними узлами, не включаемыми в число расчётных узлов системы^*) ).

3

         Посленазначения расчётных узлов и выбора рабочих гипо-тез степени подвижности узлов n_q и n_D и, следовательно, степень кинематической неопределимости n_k принимают конкретные числовые значения. Число угловых основных неизвестных n_q  определяется через число жёстких расчётных узлов n_ж.у.:

7

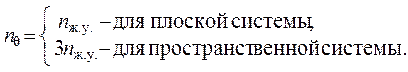                       ( 1.2 )

         Если в системе есть упругие угловые свя-

зи, то число стержней, ими соединяемых,  фор-

мально включается в  n_ж.у.. Например, для ком-  

Рис. 1.4

бинированного узла на рис. 1.2, г  n_ж.у. = 2. Для

узла, показанного на рис. 1.4,  n_ж.у. = 4.

*⁾ В стержневых системах это могут быть элементы  с «вутами»:                      ,

    Г-образные, П-образные и т.п. ломаные стержни, но их практическое приме-

    нение  не даёт существенных преимуществ  в сравнении с более простыми –

    прямыми стержнями. А вот для пластинчато-оболочечных систем, рассчиты-

    ваемых по методу конечных элементов (связь его с МП упоминалась выше),

    эффективно  применяются  весьма  разнообразные  и  зачастую  сложные  эле-

    менты.   

         При таком подходе к определению n_ж.у. каждая угловая   упругая связь рассматривается как дополнительный элемент          с жёсткостью c_q  ^*).

         Степень   линейной   подвижности n_D   ( число  независимых линейных перемещений узлов )  в общем случае,  когда в расчёте учитываются все виды деформаций элементов, находится по формуле

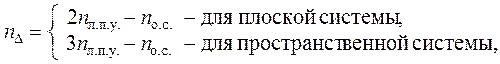           ( 1.3 )

где  n_л.п.у. – количество  линейно подвижных узлов  ( учитываются

                    все внутренние узлы системы  и  те опорные узлы,  у

                    которых есть неизвестные линейные перемещения );

          n_о.с. – число  жёстких  опорных  связей,   препятствующих

                    линейным перемещениям  ( для  каждого из узлов  на

11

                    рис. 1.2, ж, з   n_о.с. = 1 ).

         В методе перемещений традиционно используется следу-ющая рабочая гипотеза, введенная в эпоху «ручных» расчётов и порождённая стремлением к уменьшению числа основных неизвестных и снижению трудоёмкости вычислительных процедур:

для прямолинейных стержневых элементов с преобладающим изгибом можно считать пренебрежимо малым изменение расстояния между концами стержня, обусловленное

     а) искривлением элемента при его изгибе  и

     б) удлинением ( укорочением ) при растяжении ( сжатии ).      

         Краткая формулировка гипотезы: длина l ^* хорды b^*e^* деформированного элемента считается равной длине  l  стержня beв исходном – недеформированном – состоянии ( рис. 1.5 ):

l

12

                                                  .                                         ( 1.4 )  

b

e

        Следствием применения  гипотезы ( 1.4 )

b*

к  некоторому стержню является то,  что  для

e*

узлов, к которым данный элемент примыкает