Расчёт деформируемых стержневых систем методом перемещений: Методические указания к индивидуальному расчётному заданию по курсу «Строительная механика», страница 23

( 1.43.1 ) ( 1.43.2 )

        

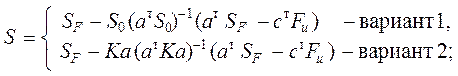
– при температурных воздействиях ( F_u = 0 ):

( 1.44.1 ) ( 1.44.2 )

                       

( 1.45.1 ) ( 1.45.2 )

– при кинематических воздействиях ( F_u = 0 ):

40б

                       

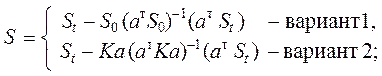
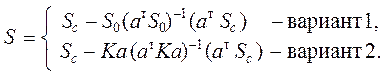
          Если требуется определить не концевые усилия S, а силовые факторы  в  специально  назначенном  наборе ,  то  вместо

зависимостей ( 1.41 ) используется

                                                                            ( 1.46 )

где – силовые факторы в единичных состояниях  и от за-

             данных воздействий – в том же наборе, что и искомые .

          При этом для вычисленияполучаются формулы

( 1.47.1 ) ( 1.47.2 )

           

52

1.6.2. Матричная проверка результатов расчёта

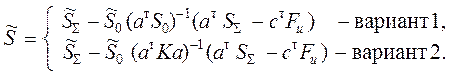
          Статическая проверка заключается в определении матрицы реакций связей, введённых в расчётные узлы, по теореме      о возможных работах концевых усилий и узловых нагрузок,       с использованием найденных усилий S:

                                                                         ( 1.48 )

54

при этом если усилия S вычислены правильно, то все компоненты матрицы реакций, имеющей n строк и n_V столбцов, должны быть равными нулю, то есть R = 0.  При компьютерном расчёте эта проверка теряет смысл, так как в ней используются те же матрицы a, c и F_u , с помощью которых ранее были определены усилия S, следовательно, по сути, проверяется только корректность выполнения компьютером матричных операций, а вероятность возникновения ошибок машинного счёта ничтожно мала.

          Кинематическая ( деформационная ) проверка – матричное вычисление перемещений по направлениям удалённых лишних связей во вспомогательной основной системе метода сил:

                           –               ( 1.49 )

результат должен быть D⁰ = 0 ( матрица размерами n_st * n_V ).  Вхо-

дящие в формулу ( 1.49 ) матрицы единичных силовых факторов ,и  в ОСМС, матрицы упругой и температурной податливости ОСМС ( B и B_t ),  матрицы  S, T и D_c ( усилий, найденных

расчётом по МП, заданных приращений температур и смещений связей ) формируются по правилам метода сил.

56

1.6.3. Приведение заданных воздействий

        к  расчётным узловым нагрузкам

          Если нагрузка состоит из сосредоточенных сил и моментов, приложенных только  к  расчётным  узлам  ( т.е. отсутствуют внеузловые нагрузки, действующие непосредственно на элементы системы ),  то  в  основной  системе  МП она не вызывает усилий в концевых сечениях стержней. Строго говоря, если расчёт выполняется с применением гипотезы , то от узловой нагрузки в стержнях возникают продольные силы, но они постоянны по длине,  следовательно,  N_bj = N_ej ,  и  поэтому  решение может строиться  с матрицами частного вида ( см. табл. 1.3 ) – без учёта сил Nи продольных перемещений концевых сечений.  Вследствие этого S_F  = 0, и формула для концевых усилий в заданной системе упрощается:

	.                        ( 1.50 )

 

          При наличии внеузловых нагрузок, а также изменений температуры и заданных смещений связей они могут быть заменены эквивалентными сосредоточенными силами и моментами в расчётных узлах так, что в результате такой замены основные неизвестные Z не изменяются. Процедура определения эквивалентных узловых нагрузок такова:

          1) с помощью стандартных  ( табличных )  данных находятся усилия S_S в элементах ОСМП ( в собственных осях координат ) от внеузловых нагрузок, изменений температуры и заданных кинематических воздействий;