Тип 3(безызгибный стержень при растяжении-сжатии)
|
общий |
Nej,…
|
|
|
||||||||||||||||||||||||||||
частныйDlj = 0 (EAj = |
Стержень учитывается как линейная связь, при отсутствии температурных воздействий в число расчётных элементов системы не включается |
|||||||||||||||||||||||||||||||
Тип 4(поперечно нагруженный
|
общий |
Nbj,… Qej,…
|
ubj,i vej,i
|
|
||||||||||||||||||||||||||||
частный
Nbj = Nej |
|
|
|
|||||||||||||||||||||||||||||
|
Матрица свободных членов КУМП ( реакций введённых связей от заданных воздействий ) вычисляется по формуле
|
где c = [ c1 c2 … ci … cn ] – матрица перемещений расчётных
узлов ОСМП во всех единичных
состояниях.
Основные неизвестные ( решение КУМП ):
|
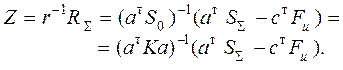 ( 1.40 )
( 1.40 )
![]() Искомые усилия в концевых сечениях элементов:
Искомые усилия в концевых сечениях элементов:
![]() . ( 1.41
)
. ( 1.41
)
Заметим, что в ( 1.41 ) aZ = D – перемещения концевых сечений, вызванные действительными перемещениями узлов Z .
Подстановка выражений ( 1.40 ) в ( 1.41 ) даёт матричные формулы для определения усилий в концевых сечениях:
|
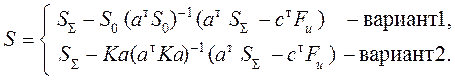
Частные случаи формул ( 1.42 ):
– при силовых воздействиях:
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.