Механика \ Строительная механика

Расчёт деформируемых стержневых систем методом перемещений: Методические указания к индивидуальному расчётному заданию по курсу «Строительная механика», страница 32

(кН * м)
 
 


D(2)= 0,01 м
 
Рис. 2.19

          Из условий равновесия узлов находятся поперечные и продольные силы, а также реакции связей Ric :

Q1,c = Q3,c = Q6,c = 0 ;  Q2,c = Q5,c = – 22,917 кН ;  Q4,c = 24 кН ;

N1,c = – N3,c = 22,917 кН ;  N2,c = 0 ;  N4,c = 75,292 кН ;  N5,c = 80 кН ;

N6,c = – 45,834 кН ;  R1c = 47,5 кН  * м ;  R2c = 137,5 кН * м ;

R3c = – 15,625 кН * м ;  R4c = 0 .

по формуле ( частный случай соотношения (1.24) ).

 

ловию =  (?)  = Rsс ,  с  определением  суммарной  реакции  Rsс

 
          Проверка правильности вычисления свободных членов уравнений   в  варианте  с  кинематическим  воздействием  –  по ус-

уже известным усилиям в нижнем концевом сечении 4-го элемента ( Mb4,s = i0  берётся с эпюры Ms на рис. 2.10 ,  Qb4,s =  = – 1,2i0  и  Nb4,s = 1,9125i0 вычисляются дополнительно ). Напомним, что положительными  считаются  реакции R(j),s , направленные в ту же сторону, что и соответствующие компоненты заданных смещений D(j) . Из  уравнений  рав-
 
Реакции смещаемых связей R(1),s ,R(2),s и R(3),s в суммарном единичном состоянии вспомогательной статически определимой системы  находим  из  равновесия  опорного  узла A  ( рис. 2.20 )  по

Nb4,s
 

Mb4,s
 
 

      

 


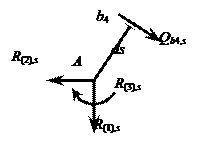                                                                             Рис. 2.20

новесия узла А  получаем  R(1),s = 2,25i0 ;

R(2),s = 0,1875i0 ;   R(3),s = i0 .  Реакция  упругой  смещаемой  связи R(4),s = – R0,s = – 2i0 . Вычисляем  Rsc = R(1),s D(1) + R(2),s D(2) + R(3),s D(3) +

+ R(4),s D(4)  = 2,25i0 * 0,02 + 0,1875i0 * 0,01 + i0 * 0,003 + ( –2i0 ) * 0,008 =

=  33,875 * 10 –3 i0  = 169, 375  и  сравниваем  с 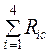= 47,5 + 137,5 –

– 15,625 + 0 = 169,375 – полное совпадение.

          Из найденных и проверенных коэффициентов и свободных членов канонических уравнений метода перемещений составляются следующие матрицы:

                      

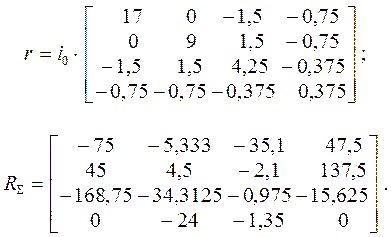
          Они могут быть использованы для определения основных неизвестных  Z = – r – 1 RS ,  но  дальнейший  расчёт  выполняется    в матричной форме с применением учебной компьютерной     программы METDEF, разработанной на кафедре строительной механики НГАСУ ( Сибстрин ).

2.4. Компьютерный расчёт рамы в матричной форме

          В программе METDEF, предназначенной для расчёта линейно деформируемых стержневых систем при многовариантных воздействиях силового, кинематического и температурного типов, реализуется вычисление искомых усилий по матричным выражениям  ( 1.42 )  и  ( 1.47 ).  Для  выполнения  расчёта  необходимо составить и ввести в компьютер исходные матрицы:

   S0  – концевых усилий в единичных состояниях ОСМП ( вместо

           S0 может формироваться – вручную или в автоматическом

           режиме – матрица K  внутренней жёсткости ОСМП );

    а  – перемещений концевых сечений элементов ОСМП  в  еди-

           ничных состояниях;

   SS – концевых  усилий  от  заданных нагрузок,  изменений тем-

           пературы и смещений связей ( по вариантам воздействий );

    с  – перемещений расчётных узлов в единичных состояниях;

   Fu – узловых нагрузок во всех вариантах заданных воздействий.

          Для  определения  усилий  в  требуемом  наборе  ( не обяза-

тельно в концевых сечениях )  по формулам ( 1.47 )  дополнитель-

но нужны матрицы и  усилий  в  назначенных  ( любых ) се-

чениях в единичных состояниях и от заданных воздействий.

          Матрицы S0 , SS , K и a формируются из блоков стандартной структуры для типовых элементов ОСМП ( см. табл. 1.3 ).

Скачать файл