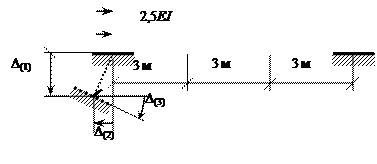Расчёт деформируемых стержневых систем методом перемещений: Методические указания к индивидуальному расчётному заданию по курсу «Строительная механика», страница 25

 

                                                                        Рис. 2.1

          Высоты сечений: стоек – h₁ = 0,3 м ;  ригелей и наклонного стержня – h₂ = 0,5 м .  Коэффициент линейного температурного расширения материала a = 12 * 10 ^{– 6} (^oC) ^–1 .

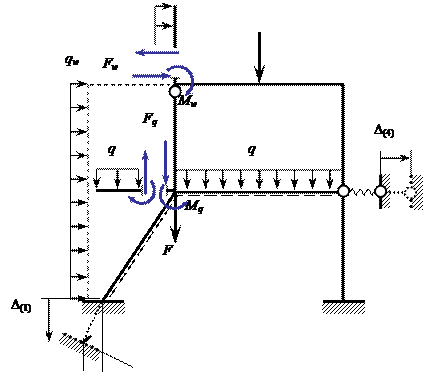
          Статически определимые консоли  ( слева и вверху )  целесообразно условно отделить, приложив к раме взамен них изгибающие моменты и поперечные силы в концевых сечениях консолей ( рис. 2.2 ).

Дополнительные нагрузки в узлах рамы: Fq = q * 2 м = 60 кН ; Mq = q * (2 м)2/2 = = 60 кН* м ; Fw = qw * 1,5 м = 12 кН ; Mw = qw * (1,5 м)2/2 = = 9 кН* м.           Степень  статиче- ской  неопределимости рамы nst = 3 * K – H = 3 *  3 – 5 = 4.

qw

F

         

 

D(3)

                     

D(2)

                                                                        

                                            Рис. 2.2    

2.2. Расчётные узлы, степень кинематической неопределимости

   и выбор основной системы метода перемещений

3

2

          Назначаем  минимально  возможное  число  расчётных  узлов – 4  ( рис. 2.3 ),  используя 1-й, 2-й и 3-й признаки из перечисленных на стр. 4.

	Жёстких узлов – два, следовательно, степень их угловой подвижности nq = 2. Легко увидеть, что независимых линейных перемещений расчётных узлов также два. Для подтверждения этого можно использовать шарнирную систему ( рис. 2.4, а ), получаемую  введением шарниров во

 

                                                                                   Рис.2.3

все жёсткие узлы,  включая опорные,

и  продольного поступательного шарнира  в  упругую  линейную

связь, отождествляемую с продольно деформируемым стержнем

( для  стержней рамы,  работающих  преимущественно  на  изгиб, применяется  гипотеза ( 1.4 ) ).

 

                                                                                  а)

 

                                                                                  

 

                                                                                 б)

                                                                           Рис. 2.4

чётные  узлы  жёстких  связей  ( рис. 2.5 )  –  двух  угловых  и  двух линейных ( в узлы 1 и 3 ),  причём линейные связи – те же, что на рис. 2.4, б.  На схеме основной системы, кроме расчётных узлов и введённых связей, обозначены также основные неизвестные – углы поворота Z₁ и Z₂ и горизонтальные перемещения Z₃ и Z₄ узлов 1 и 3^*) и элементы  ( с указанием их типов   и  концевых сечений ),  включая упругую связь, рассматриваемую как продольно деформируемый элемент.

          Нагрузка F₀ в узле 1 – сумма заданной силы F и дополнительной F_q от отделённой консоли: F₀ = F + F_q = 40 + 60 = 100 кН.

          Погонные жёсткости стержней рамы, выраженные через общий параметр:

i₁ = EI₁ / l₁ = EI / (4 м) = i₀ ;      i₂ = EI₂ / l₂ = 3EI / (6 м) = 2i₀ ;

i₃= EI₃ / l₃  = EI / (4 м) = i₀ ;       i₄= EI₄ / l₄ = 2,5EI / (5 м) = 2i₀ ;

i₅= EI₅ / l₅ = 3EI / (6 м) = 2i₀ ;    i₆ = EI₆ / l₆ = EI / (4 м) = i₀ .

          Жёсткость упругой связи: С₀ = 0,5м ^–3 * EI = 2 м ^–1 * i₀ .