Расчёт деформируемых стержневых систем методом перемещений: Методические указания к индивидуальному расчётному заданию по курсу «Строительная механика», страница 6

рис. 1.8 ), то переме-  

C

A

B

щения  узлов,  пока-

занные  на  рис. 1.7,  

станут невозможны-   

ми.    Вывод:  n_D = 2                                                                        

( совпадает  с  ранее

Рис. 1.8

полученным ).

4

                                                                       

         Для определения n_D удобно использовать вспомогательную шарнирную систему, получаемую из рассчитываемой системы путём

5

         а) введения  цилиндрических  шарниров  ( в пространственной  системе – шаровых  шарниров )  во  все  жёсткие  узлы, включая опорные защемления; а также продольных поступательных шарниров в стержни, для которых требуется  учиты-

*)  Направления  вводимых  связей  не  имеют  принципиального  значения        ( в рассматриваемом примере они лишь не могут быть вертикальными ). ).

__________________________________________________________________________________________________________________________

вать удлинения ( укорочения ) при их растяжении ( сжатии );

      б) удаления угловых  и  линейных упругих связей  ( при их наличии ), в том числе опорных.

HC

DC

а)

         Шарнирная система ( ШС ), получаемая в результате удаления связей, может быть изменяемой. Минимальное число n_д.с. линейных связей, дополнительное введение которых в узлы ШС превращает её в геометрически неизменяемую, равно искомой степени линейной подвижности расчётных узлов n_D заданной     (рассчитываемой) системы: n_D = n_д.с.. На рис. 1.9, а  показана шар-нирная система, соответствую-

B

A

C

щая рассмотренной выше раме             

( см. рис. 1.7 ),  с  дополнитель-

ными  связями  в  узлах С  и  Н,

обеспечивающими её геометри-

ческую  неизменяемость.  Заме-

б)

тим, что возможны и другие ва-

рианты размещения связей,  на-           

пример,  как  на  рис. 1.8.  В  лю-

бом случае связей  две,  то есть 

n_D = n_д.с. = 2.          

          Если  необходимо выпол

Рис. 1.9

-

нить расчёт рамы с учётом про-

дольных   деформаций   стержней   ( без   применения   допущения ( 1.4 ) ), то шарнирная система получается из варианта рис. 1.9, а  добавлением продольных поступательных шарниров во все стержни ( рис. 1.9, б ). Тогда все узлы плоской ШС оказываются фактически не связанными друг с другом, и каждый из них требует двух связей для устранения его возможных перемещений. В сумме  диый узел плоской системы требует двух               ржни может быть изменяемой.n_д.с.= n_D = 10. Такое же значение n_D получается по формуле ( 1.3 ): n_D =– 0 = 10.

         Число степеней свободы изменяемой шарнирной системы, для устранения которых требуется ввести соответствующее количество связей n_D, может вычисляться как W_ШС с использованием формулы для фермы:

3

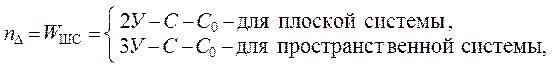  ( 1.6  )

где У, С и С₀ – количества узлов,  стержней  и  опорных связей  ( в

                         пересчёте на связи 1-го типа) шарнирной системы.

6

         При подсчёте числа стержней С элементы ШС с поступательными шарнирами не учитываются.