Расчёт деформируемых стержневых систем методом перемещений: Методические указания к индивидуальному расчётному заданию по курсу «Строительная механика», страница 31

 

3

g

D(2)= 0,01 м

D4,c = 0,0125 м

D(4) = = 0,008 м

1, 2

D(2)

41

2

D4,c

D2,c

D5,c

R3D

R3q

R1D

R1q

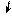
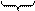
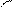
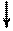
                       а)                                                                             б)

											R0,c
							1
	A

 

                        в)                                        г)

 

          Поворот опорного узла А на D₍₃₎ не вызывает смещений расчётных узлов  ( рис. 2.18, а ),  поэтому  изгиб возникает только у стержня 4, жёстко соединённого с опорой А.  Моменты М_q       ( рис. 2.18, в )  находятся  по  табл. 1.1  ( элемент  1-го типа ).   Для определения перемещений узлов от линейных смещений D₍₁₎ и D₍₂₎ опоры А  можно построить план перемещений  ( рис. 2.18, б ), с помощью которого затем отыскиваются относительные перемещения D_j,c концов стержней 2, 4 и 5 по направлениям нормалей к их осям. По величинам D_j,c далее вычисляются моменты M_D  ( рис. 2.18, г )  –  используются  данные  табл. 1.1. От горизонтального смещения D₍₄₎ деформируется только упругая связь – её реакция равна  R_0,c = – C₀ * D₍₄₎ = – 2i₀ * 0,008 = – 0,016i₀ = – 80 кН. 

90

30

137,5

137,5

R0,c = – 80 кН

(temp. 3: c)

f= 3

R1c

R3c

R4c

R2c

D(1)= 0,02 м

D(3) = 0,003

D(4) = = 0,008 м

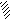
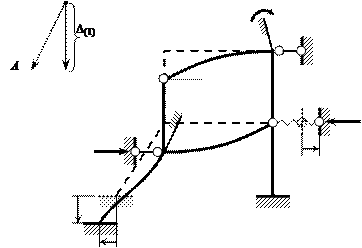
          На рис. 2.19  показаны  схема деформаций ОСМП  и  эпюра изгибающих моментов M_c = M_q + M_D от всех компонентов заданных смещений опор.

                            а)                                          б)
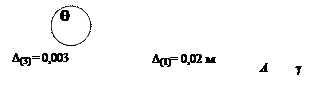
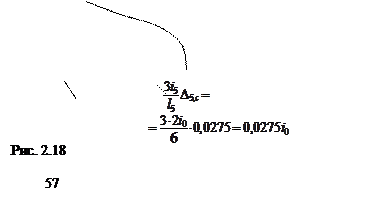