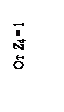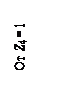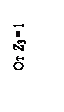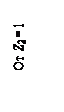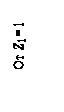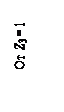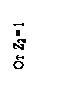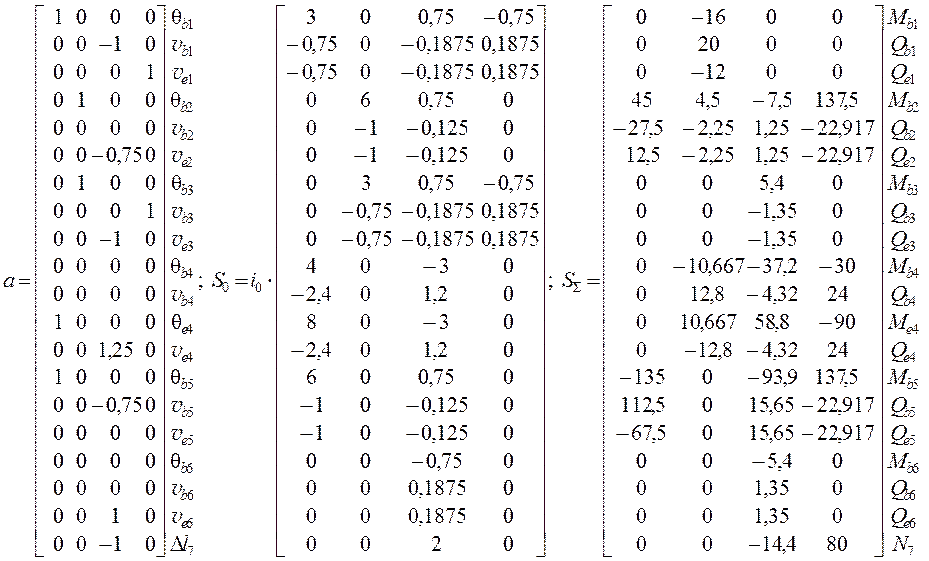условий применимости частного случая –
Dlj = 0 ( см. табл. 1.3 )
выполняется. Второе условие частного случая – требование ра-венства концевых
продольных сил – также выполняется для всех стержней, кроме 4-го элемента ОСМП, в котором нагрузка 2-го варианта ( ветровая ),
наклонная к оси стержня, вызывает продольные силы,
переменные по его длине. Но, тем не менее, и для 4-го элемента в данной задаче
может быть использован сокращённый вариант записи матриц – из-за того, что в
единичных состояниях нижний закреплённый конец стержня остаётся неподвижным,
вследствие чего продольные смещения концевых сечений ubj,i и uej,i равны нулю. Таким образом, для элементов 1, 2 , 3 , 5 и 6 ( 2-го типа )
векторы Sj,i и aj,i – трёхкомпонентные ( см. табл. 1.3 ) – в Sj,i описываются момент Mbj,i в сечении bj ( у за-щемлённого конца стержня ) и концевые поперечные силы Qbj,i и Qej,i ; а в аj,i – угол поворота qbj,i и нормальные к оси стержня линейные
перемещения vbj,i и vej,i. Для 4-го элемента ( типа 1 )
в векторах Sj,i и aj,i – по четыре компонента: соответственно Mbj,i , Qbj,i , Mеj,i , Qej,i и qbj,i , vbj,i , qbj,i , vej,i . Упругая
связь ( элемент 7 ) – 3-го типа; для
него в матрице Sj,i описывается продольная сила N7,i = – r0,i , а в матрице aj,i – абсолютная продольная деформация Dl7,i . Число строк матриц S0 и а равно 3 * 5 + 4 +
1 = 20. Все компоненты матрицы S0 содержат параметр погонной жёсткости i0 , который может быть вынесен как общий множитель матрицы.
Вводить его значение в компьютер не нужно.
Число строк и структура
столбцов матрицы SS концевых
усилий от заданных воздействий – такие же, как у матрицы S0 . Столбцов у этой матрицы столько, сколько вариантов
заданных воздействий, – в решаемой задаче 4. В первом столбце – значения
изгибающих моментов, поперечных сил и N7 от постоянной нагрузки ( 1-й вариант воздействий ), приведённые на рис. 2.11. Второй столбец –
моменты, поперечные силы и N7 2-го варианта ( от ветровой нагрузки ) – по рис. 2.12. В 3-м и
4-м столбцах – усилия от изменения
температуры ( 3-й вариант ) и смещений связей ( 4-й вариант )
– по рис. 2.17 и 2.19
соответственно.



















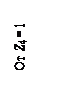
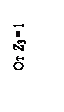
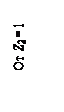
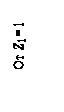
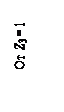
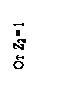
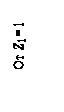








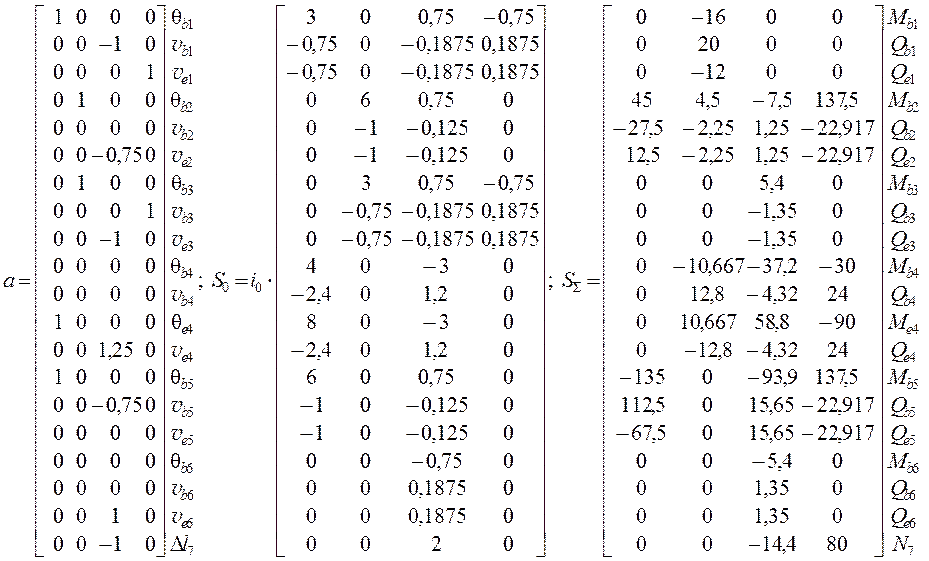
Если вместо матрицы единичных усилий S0 используется матрица внутренней жёсткости K,
то для её автоматического формирования по программе METDEF в
исходных данных должны быть описаны длины элементов и их относительные погонные
жёсткости.
Матрицы
Fu и
с
формируем, учитывая узловые нагрузки и компоненты перемещений в единичных состояниях
для четырёх расчётных узлов ОСМП – двух жёстких и двух шарнирных. В 3-м и
4-м вариантах заданных воздействий все узловые нагрузки равны нулю, а в 1-м и
2-м компоненты
Fu описываются в соответствии с расчётной схемой по
рис. 2.5. Заметим, что момент
Mw не
относится к узловым нагрузкам, так как приложен к элементу 2 и является внеузловым силовым воздействием.
При составлении матрицы
с используются схемы деформаций ОСМП (
см. рис.
2.6
).