Расчёт деформируемых стержневых систем методом перемещений: Методические указания к индивидуальному расчётному заданию по курсу «Строительная механика», страница 3

         Расчётные узлы могут быть жёсткими ( рис. 1.2, а, б ), шарнирными ( рис. 1.2, в, з )  и  комбинированными  –  рис. 1.2, г,  где совмещены жёсткий узел, соединяющий левый и вертикальный стержни, шарнирное прикрепление правого элемента и  упругоподатливое^*)  в отношении взаимного поворота  соединение левого и наклонного стержней. У опорных узлов неизвестными могут быть линейные перемещения ( рис. 1.2 ж, з ), в том числе обусловленные   податливостью  опорных  связей  ( рис. 1.2, з ),     и  углы  поворота  в  нежёстких  ( податливых )  защемлениях – рис. 1.2, и. Углы поворота концов стержней в опорных и внутренних шарнирных узлах могут не включаться в число основных неизвестных ( рис. 1.2, в, з, л;  правый элемент на рис. 1.2, г ).  Углы поворота жёсткого узла и конца наклонного стержня         в комбинированном узле  с  упругой угловой связью ( рис. 1.2, г )  должны рассматриваться как два разных основных неизвестных.

_______________________________________________________

*⁾ В общем случае соединение может быть и неупругим,  но в данных

     методических указаниях,  посвященных  расчётам  только линейно

     деформируемых систем,  этот  вопрос не рассматривается.

1.1.3. Кинематически определимые и неопределимые системы. Степень кинематической неопределимости

1

         Деформируемая система, у расчётных узлов которой есть неизвестные угловые и/или линейные перемещения, не находящиеся  из  условий  совместности деформаций  ( перемещений ) и кинематических граничных условий, называется кинематически неопределимой системой.

         Система, у которой все угловые и линейные перемещения  расчётных  узлов  известны  ( заданы  либо  равны нулю ) или могут быть найдены из условий совместности деформаций  ( перемещений )  и  кинематических  граничных  условий, называется  кинематически определимой системой.

          Представленная на рис. 1.3, а  система с абсолютно жёстким  горизонтальным стержнем  кинематически определима  ( если  рассматривать её  как  линейно  деформируемую ),  поскольку при любых силовых воздействиях её единственный узел

l

заданы

D(3)

D(1)

D(2)

q1 =D(1) / l

v1 =D(1)

 остается неподвижным  ( все компоненты его перемещений  равны нулю ),  а  при  температурных  воздействиях  или  смещениях опор вертикальное перемещение и угол поворота узла выражаются через заданные воздействия из условий совместности деформаций ( перемещений ) элементов и узлов ( рис. 1.3, б ).

 

 

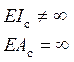                        а)                                              б)

 

                                                 Рис. 1.3

          Метод перемещений предназначен для расчётов кинематически неопределимых систем, каковыми являются подавля- ющее большинство сооружений и строительных конструкций. 

2

         Суммарное число независимых угловых и линейных перемещений расчётных узлов называется степенью кинематической неопределимости деформируемой системы:

                                           n_k = n_q + n_D ,                                       ( 1.1 )

где n_q и n_D – соответственно  степени  угловой  и  линейной  под-

                     вижности  расчётных  узлов  (количества  их незави-

                     симых угловых и линейных перемещений).