Расчёт деформируемых стержневых систем методом перемещений: Методические указания к индивидуальному расчётному заданию по курсу «Строительная механика», страница 14

34

          Вычисленные коэффициенты и свободные члены канонических уравнений должны быть проверены, для чего используется способ «перемножения» эпюр и суммарные единичные   силовые факторы – внутренние усилия S_s от одновременных единичных смещений всех связей,  введённых  в расчётные узлы

( Z₁ = 1,  Z₂ = 1, …, Z_n = 1 ),  реакции  упругих  связей  R_j,s ()   и реакции R_(j),s связей с заданными смещениями D_(j) ():

          1) собственная обобщённая суммарная единичная реакция r_ss всех введённых связей, вычисляемая по формуле

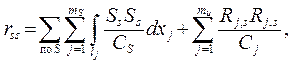                                               ( 1.20 )

должна быть равна  сумме всех коэффициентов КУМП  ( это универсальная проверка коэффициентов ):

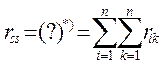                                         ;                            ( 1.21 )

          2) суммарная единичная реакция i - й связи

*) Символ (?) здесь и далее указывает на необходимость проверять     выполнение записанного условия.

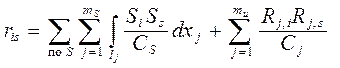                                      ( 1.22 )

 

должна  быть  равна  сумме  коэффициентов  i - го канонического уравнения ( это построчная проверка коэффициентов, производимая при невыполнении условия ( 1.21 ) ):

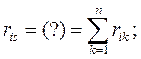                                                                          ( 1.23 )

          3) обобщённая ( суммарная ) реакция  R_sS  всех  введённых связей от заданных воздействий, вычисляемая по формуле

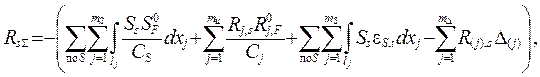 ( 1.24 )  

должна быть равна сумме всех свободных членов КУМП:

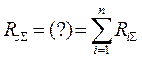                                         .                                ( 1.25 )

          Суммарные реакции r_is, r_ss , R_iS  и R_sS  можно вычислять также через возможные работы концевых усилий и узловых нагрузок:  

          Дополнительными проверками коэффициентов, основанными на использовании свойств единичных реакций связей, могут служить

          а) контроль положительности собственных реакций r_ii ;

          б) сопоставление значений пар реакций r_ik и r_ki , вычисленных различными способами и приёмами ( статическими – из условий равновесия разных узлов или частей ОСМП, либо кинематическими ) – они должны удовлетворять условию взаимности r_ik = r_ki .

27

 

1.4.4. Типовые элементы плоских стержневых ОСМП

и стандартные задачи их расчёта

          Типовые стержневые элементы в общем случае различаются  по

– способам  закрепления  концов  в  узлах  ( внутренних или опорных )  выбранной основной системы;

– виду  деформации  ( изгиб, растяжение-сжатие, сложное сопротивление );

 – закону изменения жёсткости ( при изгибе, растяжении-сжатии, кручении ) по длине стержня.  

          В плоских стержневых ОСМП выделяют четыре основных типа элементов постоянного сечения  ( рис. 1.19 ).

                             Тип 1                                        Тип 2

                      EI = const                                  EI = const

                          Тип 3                                         Тип 4

                      EA = const                                 EI = const

                                                Рис. 1.19

          Для элементов 1-го и 2-го типов возможен учёт сдвига при поперечном изгибе ( при этом считается, что GA / k_t = const );  для элементов 3-го и 4-го типа деформация сдвига в расчёте по методу перемещений не имеет значения.

          Элементы 1-го, 2-го и 4-го типов могут рассматриваться одновременно и как изгибаемые, и как продольно деформируемые с жёсткостью ЕА = const.

          Шарнир у элемента 2-го типа может располагаться на любом конце – левом или правом.

          В случае примыкания конца некоторого стержня к опорному узлу его защемление или шарнирное опирание может быть подвижным:                   или                  .

 

          Если элемент 3-го типа абсолютно жёсткий (, то при отсутствии  температурных воздействий  стержень может