Расчёт деформируемых стержневых систем методом перемещений: Методические указания к индивидуальному расчётному заданию по курсу «Строительная механика», страница 41

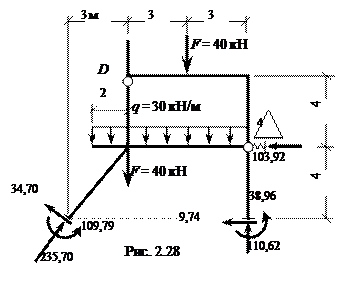
          Направления поперечных и продольных сил на рис. 2.26 соответствуют знакам на эпюрах Q_const и N_const . Нет смысла проверять выполнение условий равновесия сил в узлах, так как эти условия ранее использованы для отыскания продольных сил. Исключение  –  узел 4,  где  реакция  упругой  связи  ( продольная сила в ней ) получена  в  результате  компьютерного  расчёта.  Для этого узла вычисляем Sx₍₄₎ = 106,01 +7,65 – 103,92 – 9,74 = 0,00 кН.

Для отсеченной части   ( рис. 2.27,  где сечения про-   ходят бесконечно близко  к   узлам рамы ):   = –7,65 + 7,65 –    –103,92 – 9,74 +     =       =149,07 – 149,07 = 0,00;   = –14,90 – 25,10 – – 60 +   – 40 + 110,62 = = 320,00 – 320,00 = 0,00;

14,90

25,10

          Более надёжными являются проверки равновесия отсеченных частей и рамы в целом. Значения и знаки внутренних силовых факторов определяются  по эпюрам  M_const , Q_const  и  N_const.

 

                         Рис. 2.27  

         = 30,62 + 60 – 63,71 + (14,9 + 60 + 40

–= = 1885,70 – 1885,67 = 0,03 кН* м ( с погрешностью 0,0016% ).

          Для всей рамы, отделенной от диска «земля» сечением по всем опорным связям, включая упругую в узле 4 ( рис. 2.28 ):

 

53

          Второй этап  проверки результатов расчёта – кинематическая  ( деформационная )  проверка  –  выполняется  с  использованием статически определимой основной системы метода сил, в которой определяются суммарные единичные усилия от Х₁ = 1,  Х₂ = 1, …, Х_n = 1 ( рис. 2.29 ).

 

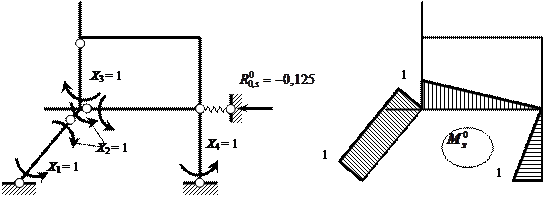                                               Рис. 2.29

          Обобщённое перемещение по направлениям лишних связей, которое при отсутствии ошибок в результатах расчёта должно быть равным нулю, находим по формуле, получающейся  из  ( 1.30 )  как  частный  случай  для  рассматриваемой  рамы с одной упругой опорной связью:     

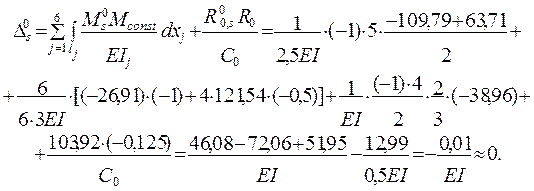
          Вывод: полная проверка результатов расчёта рамы на действие постоянной нагрузки свидетельствует о корректности решения задачи.

56

2.4.6. Вариант расчёта с заменой внеузловых воздействий

                       расчётными узловыми нагрузками

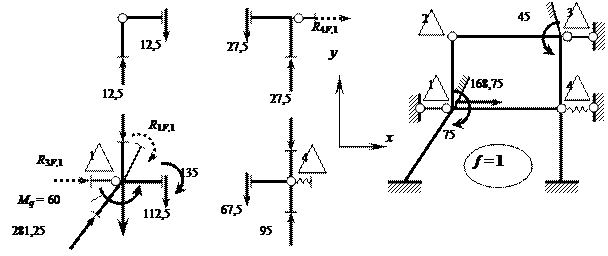
          Для определения расчётных узловых нагрузок в каждом из вариантов заданных воздействий, в соответствии с изложенным в п. 1.3.6 алгоритмом, рассматриваются расчётные узлы ОСМП  с приложенными к ним заданными узловыми нагрузками и дополнительно – концевыми усилиями примыкающих к узлам элементов, возникшими от внеузловых нагрузок, изменений температуры и смещений связей. В случае постоянной нагрузки, использовав данные рис. 2.11, получаем схемы узлов, приведенные на рис. 2.30, а  ( показаны только отличные от нуля усилия ).

45

3

R2F,1

2

                              а)                                                      б)

 

F0 = 100

                                                        Рис. 2.30 

          Суммируя приложенные к каждому узлу моменты и проекции сил, параллельные глобальным осям х и у, находим расчётные узловые нагрузки первого варианта воздействий ( f  = 1 ) – рис. 2.30, б.