*)
Z3 – горизонтальная ( по направлению введённой линейной связи )
проекция полного перемещения узла 1, происходящего по нормали к оси 4-го
элемента.
*)
Z3 – горизонтальная ( по направлению введённой линейной связи )
проекция полного перемещения узла 1, происходящего по нормали к оси 4-го
элемента.
Рис. 2.5
2.3. Канонические уравнения. Определение и проверка
коэффициентов и свободных членов
Для выбранной основной системы канонические уравнения метода перемещений имеют
следующий вид:
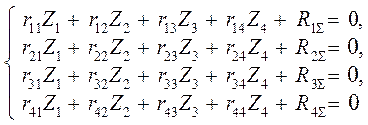
или
в матричной форме:
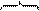
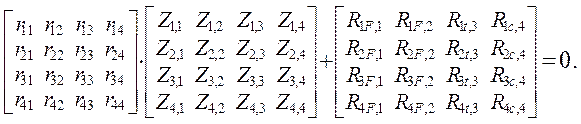
 По вариантам заданных воздействий:
По вариантам заданных воздействий:
– вариант 1 – постоянная нагрузка,
– вариант 2 – ветровая нагрузка (1-я временная),
– вариант 3 – изменение температуры (2-я временная),
– вариант 2 – смещения опорных связей (3-я временная).
2.3.1. Единичные состояния основной системы.
Определение и проверка коэффициентов КУМП
На
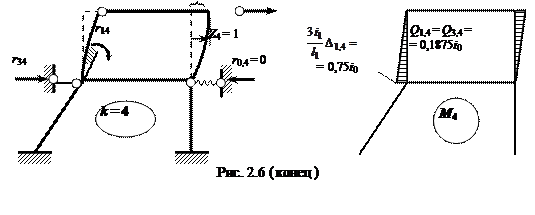
рис. 2.6 представлены схемы деформаций основной си-стемы от единичных
смещений введённых
связей (
от единичных основных неизвестных
Z1 = 1, …,
Z4 = 1
) и соответствующие
им эпюры изгибающих моментов, при построении которых использованы данные табл.
1.1. Рядом с эпюрами даны значения поперечных сил
Qj,k (
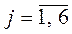
– номера
изгибаемых элементов ОСМП,
k – номера единичных состояний
). В
единичных состояниях перемещения и деформации элементов таковы, что выполняются
условия их совместности в узлах и кинематические граничные условия в опорных
закреплениях.











а)
б)
Рис.2.6 ( начало )
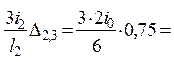
= 0,75i0
|
|


План перемещений
расчётных узлов
|
|














в)
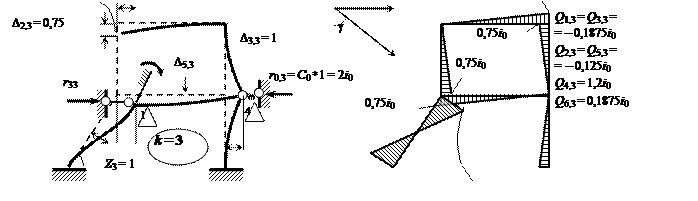

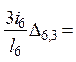 0,75i0 0,75i0
|
|


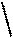


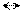





г)
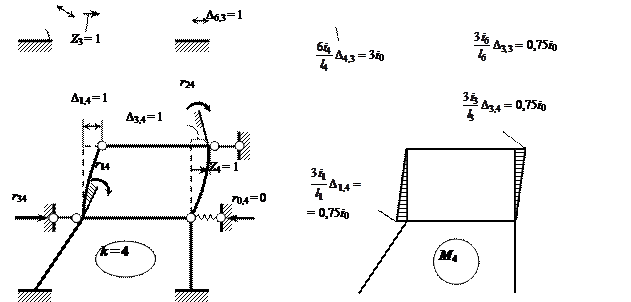
Для построения плана перемещений расчётных узлов от единичного смещения
3-й (
линейной ) связи (
рис. 2.6, в ) можно
использовать шарнирную систему.
![]() *)
Z3 – горизонтальная ( по направлению введённой линейной связи )
проекция полного перемещения узла 1, происходящего по нормали к оси 4-го
элемента.
*)
Z3 – горизонтальная ( по направлению введённой линейной связи )
проекция полного перемещения узла 1, происходящего по нормали к оси 4-го
элемента. 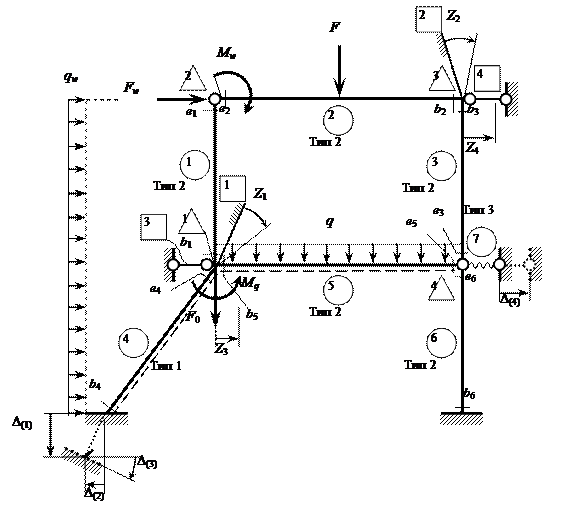
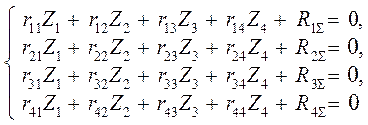
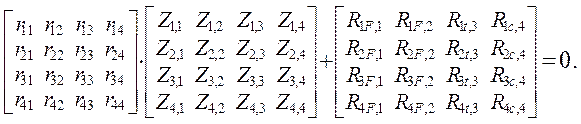
![]() По вариантам заданных воздействий:
По вариантам заданных воздействий:


 а)
а)

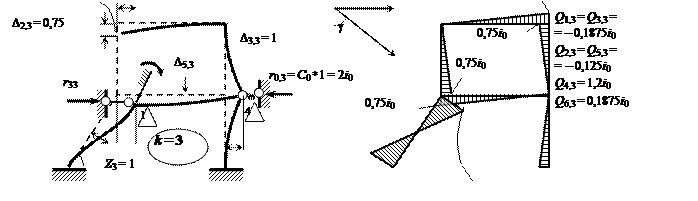
![]()
![]()
![]()
![]()