Рис. 2.15
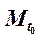 МF,2 МF,2
|
|















































Равномерная составляющая D
t0 изменения температуры вы-зывает
удлинения 4-го и 5-го элементов D
l4t =
a
D
t04 l4 =
1,2 * 10
–3 м
и D
l5t =
a
D
t05 l5 =
1,44 * 10
–3 м, вследствие чего возникают перемещения узлов ОСМП (
рис. 2.16, а
),
для определения которых можно использовать план перемещений.
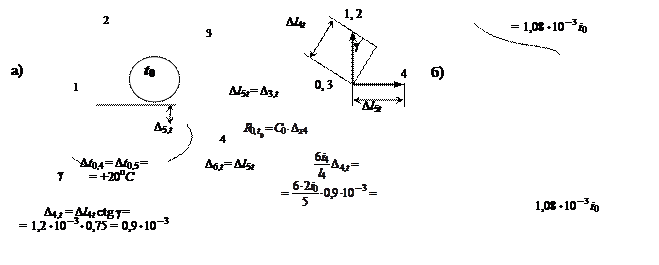
D2,t = D5,t = Dl4t /cos g = 1,5 * 10 – 3
|
|
Изгибающие моменты от Dt0 , найденные по формулам табл. 1.1 подстановкой в них
значений относительных смещений концевых сечений элементов Dj,t по нормали к продольной оси, представлены на рис. 2.16, б. Объединив ( суммировав ) перемещения и моменты от Dtnr и Dt0 , получаем деформированное состояние ОСМП, показанное
на рис. 2.17, а, и эпюру полных
изгибающих моментов Mt = 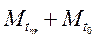 ,
вызванных изменением
,
вызванных изменением
температуры
Dt = Dtnr +
Dt0 ( рис. 2.17,
б ). Вычисление Mt выполняется с
использованием значения параметра погонной жёсткости i0 = EI/( 4 м ) =
2 * 104
кН * м2/( 4 м ) =
5000 кН * м .



а) б)
Рис. 2.17
Соответствующие поперечные силы: Q1,t = 0; Q2,t = 1,25 кН;
Q3,t
= – 1,35 кН; Q4,t
= – 4,32 кН; Q5,t = 15,65 кН; Q6,t
= 1,35
кН; реакция упругой связи R0,t = C0 * Dx4
= 2i0 * 1,44*10 – 3 = 14,4 кН.
По найденным силовым факторам статическим методом ( способом
вырезания узлов ) определяем
реакции введённых
свя-зей: R1t
= – 35,1 кН * м; R2t
= – 2,1 кН * м ( из равновесия моментов в узлах 1 и 3 ); R3t =
– 0,975 кН; R4t =
– 1,35 кН
(
последовательным вырезанием узлов
2, 3, 4, 1 ).
Для их проверки используем
условие 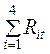 = (?) = Rst , где
= (?) = Rst , где
Rst
вычисляется с помощью формулы ( 1.24 ), из
которой для плоской стержневой системы в случае
температурного воздействия
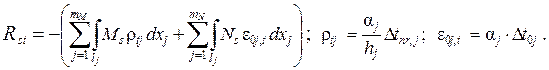
Продольные силы в элементах 4 и 5 в суммарном единичном
состоянии ОСМП: Ns,4 = 1,9125 i0 ; Ns,5 = – 2,9375 i0
.
Температурные деформации стержней:
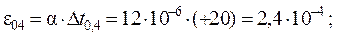
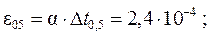
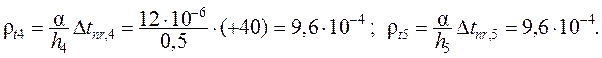
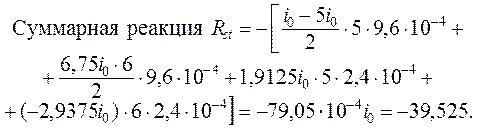
Сумма свободных членов КУМП ( реакций Rit от заданного
температурного воздействия ) 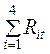 = – 35,1 – 2,1 – 0,975 – 1,35 =
= – 35,1 – 2,1 – 0,975 – 1,35 =
=
– 39,525 – точно совпадает с Rst ,
следовательно, величины Rit вычислены
правильно.
Для определения реакций
введённых связей в 4-м варианте заданных воздействий (
от
смещений опорных связей
) отдельно рассматриваются угловые и линейные
перемещения опор (
рис. 2.18, а, б
). На схемах обозначены
только отличные от нуля реакции связей.





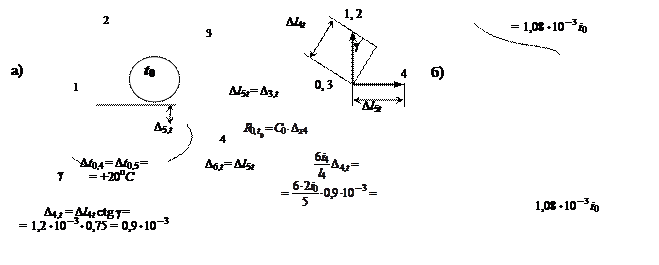
![]() ,
вызванных изменением
,
вызванных изменением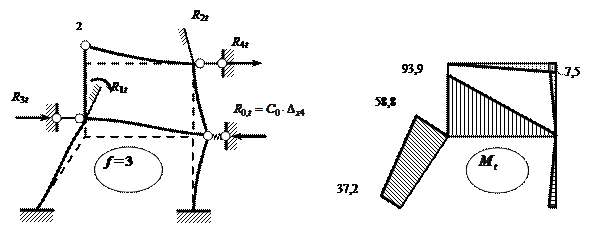
![]()
![]()
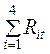 = (?) = Rst , где
= (?) = Rst , где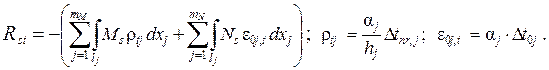
![]()
![]()
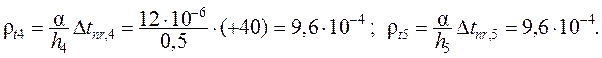
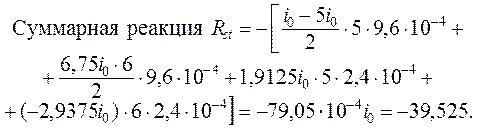
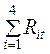 = – 35,1 – 2,1 – 0,975 – 1,35 =
= – 35,1 – 2,1 – 0,975 – 1,35 =