Физика \ Тепломассообмен

Тепломассообмен (физико-математические основы): Учебное пособие, страница 9

В  качестве  падающих  обычно  бывают  эффективные  потоки  от  других  тел  системы,  но  на  рассматриваемую  поверхность  они  попадают  не  полностью  а  частично.  Отношение  части  эффективного  потока,  попавшей  на  какую – либо  поверхность,  ко  всему  эффективному  потоку   называют  угловым  коэффициентом.  В  системе  из  двух  тел  в  лучепрозрачной  (не поглощающей)  среде  два  эффективных  потока -  Q э1  и  Q э2 .  Если   часть  Q э1, например  Q12,  попадает  на  поверхность  второго  тела,  то  угловой  коэффициент  излучения  с  первой  поверхности  на  вторую  j12 = Q12/Qэ1,  а  угловой  коэффициент  излучения  со  второй  поверхности  на  первую   j21 = Q21/Qэ2 .

Определенные  таким  образом  коэффициенты  называются   средними.   Различают  также  элементарный  и  локальный  угловые  коэффициенты:  элементарный  коэффициент  определяет  условия  теплообмена  излучением  между  двумя  элементарными  площадками  dF1  и  dF2;  локальный  коэффициент  определяет  такие  же  условия   для  системы  из  элементарной  площадки  dF1  и  полной  поверхности  F2.  В  замкнутой  системе  из   n  поверхностей  с  лучепрозрачной  средой  для  учёта  многократных  отражений  используют   разрешающие  угловые  коэффициенты.

Если   В1 -  энергетическая  яркость  излучения  поверхности  F1  в  точке  А (спектральная  или  интегральная),  то  dq1u = B1 dw1 cos u1 -  есть 

      a)                  dF2                             b

                                       bB                                   n1

     n 2

u2                                                                                        u1

                                                             b)                                 

            n1                              dw1                                                                                   du1

                                                                        r                                      r d1

                    u1                        r

                                                                                           

                                                                                                                d

                                                                          r

  dF1                              a                                         o                               f

                              f                                                                            

                                                                                                     df

Рисунок 3. -  Схемы  к  определению угловых  коэффициентов.

плотность потока  излучения  в  направлении  угла  u1  по  нормали  n1.  Из  тригонометрии  известно,  что  величина  телесного  угла  определяется  отношением  площади,  вырезываемой  на  поверхности  сферы  этим  углом,  к  квадрату  радиуса  сферы,  поэтому по  рисунку 3а         d1= d F2 ×cos u2/ r2.  Тогда            dQ1u = dq1 dF1 = B1×cos u 1 × cos u2 ×dF1×dF2/ r2 .

Для  определения  полного  потока  излучения  в  полупространство   dQ1 нужно  dQ1u  проинтегрировать  по  полусфере  радиусом   r. 

Из  рисунка 3b

dw1= r×du1×r×df/ r2 = r×du1×r×sin u1×df / r2 = sin u1×du1 ×df

и              dQ1u= B1×dF1×cos u1×du1×sinu1×df  = B1×dF1×sinu1×d (sinu1)×df.

Интегрируя  это  выражение  в  пределах  f =0…2p , u1 = 0…p /2,  получим  dQ1 = B1×p×dF1.

Элементарный  угловой  коэффициент  излучения с   dF1  на  dF2

j(dF1,dF2)=    Аналогично    j(dF2,dF1) =

Отсюда  видно,  что

j(dF1,dF2) dF1 = j(dF2,dF1) dF2.

Это  равенство  иллюстрирует  так  называемое  свойство  взаимности  угловых коэффициентов.

Локальные  угловые  коэффициенты  для  системы  dF1  и  F2  опреде-ляются  формулами

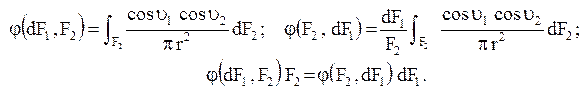
Средние  угловые  коэффициенты  системы  из  F1 и F2

В  этом  случае,  как  и  в  предыдущем,  сохраняется  равенство
Скачать файл