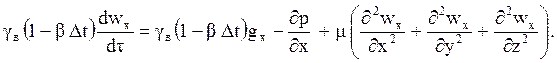
![]()
Здесь gв - плотность среды вдали от стенки;
Dt - перепад температуры между поверхностью стенки и средой вдали от неё;
b - коэффициент объёмного расширения среды.
Решение этого уравнения позволяет получить уравнение распределения скоростей в потоке, а при нестационарном режиме - и изменение их во времени.
В теории движения сред различают ламинарный и турбулентный режимы течения. В первом случае частицы среды следуют в потоке по вполне определенным главным траекториям, все время сохраняя движение в направлении вектора средней скорости потока, а возникающие в потоке случайные нерегулярности гасятся. Во втором случае в потоке возникают пульсации скорости, в том числе и поперечные, отдельные объёмы среды перемещаются и поперёк потока. В нём возникают вихри.
Если
осредненные по времени скорости течения среды не изменяются во
времени или изменяются медленно, то действительную скорость можно
представить в виде суммы w =![]() + w¢, в
которой
+ w¢, в
которой ![]() – вектор осредненной
скорости, а w¢ - вектор пульсационной составляющей истинной
скорости, дающий отклонение скорости по величине и направлению от
осредненного значения.
– вектор осредненной
скорости, а w¢ - вектор пульсационной составляющей истинной
скорости, дающий отклонение скорости по величине и направлению от
осредненного значения.
Пульсации скорости вызывают появление новых слагаемых в правых частях уравнений движения, по смыслу аналогичных членам уравнений, обусловленным силами вязкого трения. Поэтому структура уравнений еще более усложняется, а система этих уравнений оказывается незамкнутой. Для её замыкания используют дополнительные гипотезы из области полуэмпирических теорий турбулентности.
Деление потока на ядро и пограничный слой позволяет рассматривать каждую из этих областей в отдельности.
В ядре потока силы инерции преобладают над силами вязкостного трения, поэтому для описания движения можно пользоваться уравнениями идеальной жидкости (среды). А в пограничном слое преобладают силы вязкости, поэтому движение в нём описывается упрощенными дифференциальными уравнениями, которые можно интегрировать. Вопросы, связанные с выводом и решением таких уравнений рассматриваются в особой теории пограничного слоя.
Раздельный анализ упрощенных уравнений с последующим смыканием полученных решений для ядра потока и пограничного слоя позволяет получить все необходимые характеристики потока в целом.
2.4. Уравнение конвективного теплопереноса. Уравнение
теплопроводности
Вывод уравнений базируется на законе сохранения энергии. Он, как и вывод уравнения неразрывности, начинается с определения приращения количества, но не массы, а потока тепловой энергии, плотность которого по оси х в пределах объёма dV меняется от q x до q x + (¶q x/¶x) dl x .
Приращение количества тепла в направлении оси х
dQx = dQx1 - dQx2 = [q x - q x – (¶q x/¶x) dl x]dl ydl zdt = - (¶q x/¶x) dV dt .
Плотность теплового потока при конвективном тепломассообмене
q x = - l(¶ t /¶x) + g wx i , поэтому после подстановки получим
dQx = [l(¶2t/¶x2) - g wx(¶ i/¶x) - g i (¶wx/¶x)] dV dt .
Определяя таким же образом приращения тепловых потоков по остальным осям и суммируя их, получим
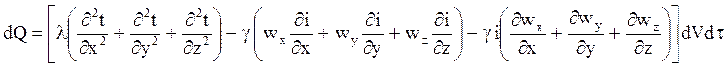 .
.
Анализируя уравнение неразрывности потока, мы пришли к выводу, что при g = const сумма последней скобки в выше приведенной формуле равна нулю.
Если процесс теплопереноса происходит при постоянном давлении, что имеет место в большинстве теплотехнологических агрегатов, то всё приращение тепла dQ расходуется на изменение энтальпии объёма:
dQ = g dV(¶i /¶t).
Учитывая, что ¶i = cp ¶t и приравнивая правые части двух выражений для dQ, после деления на g ср dV, получим уравнение переноса энергии
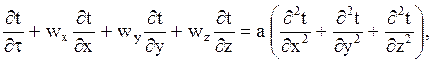
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.