Тепломассообмен (физико-математические основы): Учебное пособие, страница 53

Q_ci = A_i Q_эi – R_i Q_pi  -  для  поверхностных  зон  II-ого  рода;

Q_pi = A_ci   -  для  объемных  зон  I-ого  рода;

Q_ci = Q_эi,  где  i = N+m₁+1,…,N+M ,  для  объемных  зон  II-ого  рода.

Зная  собственные  лучистые  потоки  зон,  можно  найти  и  их  температуры.

Как  видно,  в  этом  случае  приходится  пользоваться  четырьмя  типами  уравнений.  Системы  таких  уравнений  получаются  довольно  сложными.

В  резольвентном  методе  из  расчетных  уравнений  исключаются   промежуточные  звенья – эффективные  лучистые  потоки. При этом  перенос  энергии  как  для  поверхностных,  так  и  для  объемных  зон  описывается  единообразно.

Резольвентой  называют  отношение  элементарного  лучистого  по-тока  с  площадки  dF_k,  попавшего  на  единичную  поверхность  в  точке  N  с  учетом  многократных отражений от границ  системы, к  элементар-ному  полусферическому потоку собственного  излучения  с площадки dF_k.  Это  отношение  равно  отношению  элементарного  разрешающего  угло-вого  коэффициента  dΨ_kn  с  площадки  dF_k на  площадку  dF_n   к  самой  площадке dF_k. 

Основным является  уравнение  Q_p = Q_пг – Q_c = Q_п A – Q_c . Падающий  поток  излучения  выражают через  собственный  поток  и  через  разреша-ющий  угловой  коэффициент:  Q_пi = поэтому результирующие  лучистые  потоки  для  зон I-ого  рода,  как  поверхностных,  так  и  объем-  ных,  выражаются  одним  уравнением    Q_pi = A_i,

а  для  зон   II-ого  рода        Q_ci = A_i .

Как  видно,  здесь  только  две  формулы,  содержащие  одинаковые  величины,  но  с  переставленными  Q_pi  и  Q_ci .  Ясно,  что  решение  систем  этих  уравнений  проще,  чем  по  классическому  методу.  Кроме  того,  если  для  всех  зон  заданы  температуры,  то  есть  плотности   собственных  потоков  излучения,  то  решение  задачи  сводится  просто  к  вычислениям  результирующих  по-токов  Q_pi.  А  при  задании  Q_pi  cистема  уравнений  имеет  бесчисленное  множество  решений.

При  явной  простоте  этой  системы  решение  ее  не  так  уж  просто,  потому  что  предварительно  нужно  рассчитать  разрешающие   угловые  коэффициенты, используя систему  уравнений  вида   а  при  значениях  степени  черноты  поверхностей  в  пределах  0,8…1,0  можно  использовать  два-три  члена  ряда из  формулы, получаемой  мето-  дом  многократных  отражений:

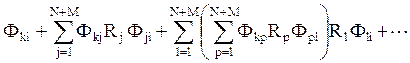
При  большом  количестве  зон   решение  всех  систем  уравнений  прихо- дится осуществлять с помощью вычислительных машин. Тогда, во-первых, лучше  использовать  матричную  алгебру,  а  во-вторых,  угловые  коэф-фициенты  определять  методом  Монте- Карло.  В  настоящее  время  раз-работан  ряд  методик  его  применения.  Ю.А. Журавлевым, В. Г. Лисиен-ко  и  Б. И. Китаевым  показано,  что  при  задании  в  модели  диффузного  закона  излучения  и  отражения,  а  также  при  условии  изотропности  из-лучения  в  объеме  среды,  метод  Монте-Карло  целесообразно  использо-вать  лишь  для  определения  обобщенных  угловых  коэффициентов,  а  разрешающие  находить  путем  решения  вышеуказанной  системы  уравнений,   также  прибегая  к  матричной  алгебре.

3.10.  Решение  задач  сложного  теплообмена

В  реальных  теплотехнологических  устройствах  теплообмен  в  большинстве  случаев  происходит  одновременно  излучением  и  конвекцией,  потому  что  наличие  разности  температур  вызывает  свободное  движение  среды  около  твердых  поверхностей,  если  даже  нет  побудителей  типа  горелок,  форсунок,  дымовых  труб  и  других  отсасывающих  или  нагнетающих  устройств.

Только  в  тонких прослойках  при  критерии Релея  Ra=Gr Pr,  мень-шем  или  равном  определенному  критическому  значению,  свободная  конвекция  гасится  силами  вязкости  среды,  и  теплоперенос  в  ней  про-исходит  теплопроводностью  и  излучением,  если  среда  прозрачна  или  полупрозрачна.  Через  жидкостные  прослойки  теплоперенос  происходит  только  конвекцией  или  теплопроводностью,  в  зависимости  также  от  величины  критерия  Релея.  В  вакуумных  системах,  даже  при  высоком  вакууме,  теплоперенос  происходит  за  счет  движения  среды  на  молеку-лярном  уровне  и,  конечно,  излучением.