Тепломассообмен (физико-математические основы): Учебное пособие, страница 44

Но  кроме  этих  имеется    ещё   ряд схем-шаблонов которые  обладают  своими  достоинствами  и  недостатками,  например,  явная  абсолютно  устойчивая  схема  Дюфорта  и  Франкела

                                                              ¨t _n,t+1

                                       t _n-1,t·           ·           · t _n+1,t

· t _{n, t-1}

и  другие [3].  В  этом  же источнике  показаны  шаблоны  для  решения  одномерного  уравнения  теплопереноса  в  потоке  среды (конвективный  теплообмен).

Как видно из вышеизложенного, замена  дифференциальных опера-торов поставленной задачи конечно-разностными оказывается не одноз-начной, допускающей некоторый произвол. Так первую производную функции t в прямоугольной системе координат  можно заменить следующими  разностными выражениями:

Первое из них называется правым  разностным отношением, второе – ле- вым разностным отношением, а третье – центральным. Можно применять и комбинированное выражение

, в котором σ – так называемый весовой коэффициент. Если он равен едини-це, то получается первое отношение, если нулю, то получится второе отно-шение, а если σ = 0,5, то получится третье отношение.

Вторую  производную также  можно  заменить  различными  разнос- тными  отношениями,  но  чаще  всего  ее заменяют через правую и левую разности  в  виде

.

Как мы  уже  видели,  производную  можно  выражать  и явно, и неявно.

В общем  случае неважно как организована  замена,  важно  чтобы  она обеспечивала  устойчивость  решения и совпадение  результатов  приб-лиженного решения  с  результатами точного при уменьшении  шагов  по   времени  и по координатам  до нуля. Если  это  условие выполняется, то  разностное решение  называют сходящимся  к  точному. Можно  сказать, что сходимостью обладают  разностные  схемы, которые  аппроксимируют  исходную  задачу и являются  устойчивыми.

Степень  аппроксимации определяется погрешностью, то  есть  раз-ницей между  результатом  точного  и  приближенного  решения. Если  использовать  ранее полученные  выражения для t_n+1 и t_n-1 путем  разложе-ния  в  ряд  Тейлора,  то  можно  получить

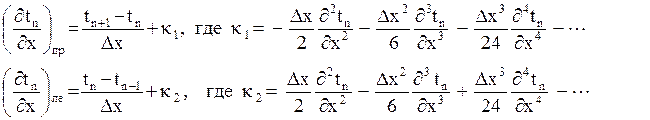
Здесь κ₁ и  κ₂ – погрешности  разностного  решения.

Если, как  мы  делали, оставить  производные  только первого  порядка,  то погрешности окажутся прямо  пропорциональными Δх, то есть они  будут  иметь первый  порядок малости П(Δх). 

Если  сумму  правой  и  левой  производных поделить  пополам,  то  получится выражение  для  центральной  разности

, то  есть погрешность  имеет порядок  малости П(Δх²). Погрешность разно-стного решения  второй производной κ₄ = κ₁ – κ₂ =   то  есть  также  имеет  П(Δх²).

Чем  выше  порядок  аппроксимации  производной,  тем  точнее  решение.

Кроме того,  еще  различается  невязка  для  всего  разностного  урав-нения.Она  представляется,  например,  так:

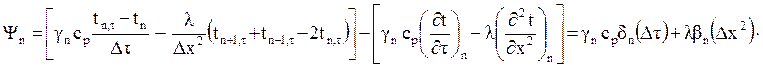Эта  невязка  называется  погрешностью  аппроксимации  исходного  диф-ференциального уравнения  конечно-разностным  уравнением. Полученное  выше  выражение  показывает,  что порядок  точности  данной  схемы  апп-роксимации  П(Δτ+Δx²) равен 1 по времени  и  2 – по пространственной ко-ординате. Таким же  образом  проверяется  точность  аппроксимации  гра-ничных  условий.  И  если  для  них порядок  аппроксимации  по  коорди-нате  равен  1,  то в  целом  для  разностной  схемы  будет Ψ_n=П(Δτ+Δx),  то  есть  будет  равен 1 по  обоим  параметрам.

Для характеристики погрешности  численного  решения во  всех  расчетных  точках   вводят  одно  какое-либо  число,  которое  называют  нормой  погрешности ‌ ‌ κ_n ‌ ‌ .  Например,  ее  можно  определить  просто как  ‌‌ ‌ ‌ κ_n‌ ‌ = max‌ κ_n‌ , а можно и  сложнее: ‌ ‌ κ_n ‌ ‌ = Σ ‌ κ_n ‌ .  Для  характеристики погрешности аппроксимации всей разностной схемы вводят ее норму  ‌ ‌Ψ_n‌ ‌, определяемую  аналогично.                                                                                         Тогда условия устойчивости решения записываются как ‌ ‌ κ_n ‌ ‌ ≤ ς ‌ ‌Ψ_n ‌ ‌ при достаточно  малых Δτ  и  Δx, и постоянной ς, не  зависящей от  двух  последних.