Тепломассообмен (физико-математические основы): Учебное пособие, страница 42

Первый из них  -  формальная  замена  производных  путём  разложения  функции  в  ряд   Тейлора.  Для  примера  возьмём  дифференциальное  уравнение  теплопроводности  в  бесконечной  пластине  при  g с_р = const   и     l = var :    Пластину  разобьём  по  толщине  на  целое  число  слоёв  толщиной  Dх.  В  центральной  плоскости  одного     из   слоёв,  или  на  границе  слоя  температуру    обозначим  через  t_n; слева  от неё  на   расстоянии  Dх  температуру  обозначим  через  t_n-1,  а  справа  на  таком  же расстоянии  -  через t _n+1,  (рисунок  17).

                            D х                    D х                 Dх

                                                                             t _n+1

·  

t _n

·

t _n-1

·

Рисунок  17. – Схема  разбиения  пластины  на  слои.

С  помощью  ряда   Тейлора  выразим  t _n-1,  и  t _n+1,  через  t _n:

Отнимая   t _n-1   от    t _n+1,  получим

Оставляя  производные до  второго  порядка,  получим (¶t _n/¶x)@(t_n+1 –  -  t_n-1)/2Dx .  Аналогично  будет  выглядеть  и  ∂λ/∂х.

Суммирование  t_n+1  и  t_n-1  даёт  (t_n+1 + t_n-1) = 2 t _n + (¶²t_n/¶x²) Dx²,  или

(¶²t_n/¶x²) = ( t _n+1 + t _n-1 – 2 t _n) / Dx².

Используя  эти  выражения  и  обозначая  температуру  точки  n  по  истечении  промежутка  времени  Dt  через  t _n,t,   уравнение теплопровод-  ности  в  конечно-разностной  форме  запишем  в  виде

Отсюда   температура  в  точке  n  через  промежуток  времени  Dt

При  заданных  начальных  условиях  начальное  распределение  температуры  известно,  и  по  нему  можно  рассчитать  распределение  через  промежуток  времени  Dt,  используя  приведенную  выше  формулу.   Принимая  это  распределение  за  начальное,  можно  таким  же  образом  рассчитать  распределение  температуры  в  конце  второго  интервала времени  Dt,  затем  -  в  конце  третьего  и  так  далее.   Как видно,  в  этой  схеме  неизвестные  значения  температуры  рассчитываются  по  уже  известным,  поэтому  такая  схема  расчёта  называется  явной.

Но можно,  оставив  левую  часть  уравнения  той  же  самой,  только  поменяв  индексы  у  g  и  с_р  на  (n,t),  правую  часть  выразить  через  температуры,  которые  будут,  через  промежуток  времени    Dt,  то  есть  через  t _n,t  t _n+1,t  t _n-1,t .  Тогда  расчётная  формула  будет  иметь  вид

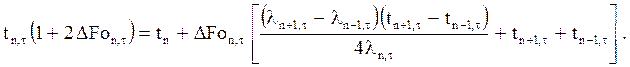
Такая схема расчёта называется неявной.   Как  видно,  в приведенной  формуле  только  одна    известная   температура  t _n   и  три   (t _n,t, t _n-1,t,  t _n+1,t)   неизвестных.  Кроме  них  неизвестными,  следовательно,  будут  l _n,t ,  l _n-1,t ,   l _n+1,t ,  как  зависящие  от  температуры.  То  есть  решение  задач  по  такой  схеме  будет  затруднительным,  так  как  на  каждом  временном  шаге  нужно  будет  решать  систему  уравнений,  а  их  количество  может  достигать  нескольких  десятков.   Казалось  бы,  что  поэтому  лучше  использовать  предыдущую,  явную,  схему  расчёта.   Но  она,  оказывается,  имеет  скрытый  недостаток,  который  заключается  в  неустойчивости  решения.  Эта   неустойчивость  проявляется  в  том,  что  изменение  температуры  во  времени получается не гладким, монотонным, а с колеба-  ниями,  амплитуда  которых  со  временем  увеличивается. Эти  значения  температуры  могут  не  соответствовать  физическому  смыслу  задачи.  Пример   устойчивого  и  неустойчивого  решения  одной  и  той  же  задачи  при  граничных  условиях  первого  рода  приведен  в  таблице  3.

Таблица  3. – Устойчивое (слева)  и  неустойчивое (справа)  решение задачи  по  двухстороннему  нагреву  пластины.

   Dt                             n                                                       n

             1           2          3           4          5          1          2        3          4         5

0     (80)        43,0    27,5   22,0     (20,0)      (80)      43,0    27,5     22,0      (20)