Тепломассообмен (физико-математические основы): Учебное пособие, страница 48

Если  же  известны  его  дискретные  значения  в  виде  таблиц,  то  усреднен-ную  величину  можно  найти  из  условия  равенства  общего  теплового  соп-ротивления  сумме  последовательных  сопротивлений. Так  для  двухслойной  плоской  стенки                .

Здесь  δ_Σ = δ_i + δ_i+1 – суммарная  толщина  стенки;

λ_i , λ_i+1 – коэффициенты  теплопроводности  слоев  стенки. Если  слои  из  одного  материала, то  λ_i и λ_i+1 принимать  по  температу –

рам  t_i и t_i+1.

Окончательно,  после  преобразований этого  равенства, например  для  участка  0-5  получается

.

Если  правая  плоскость  ΔV  располагается  по  средине  сектора  n-(n-1), то  Δφ_n-1= 2φ₂, и  тогда

.

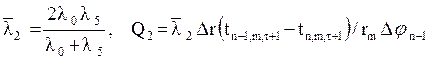а  все  конечно-разностное  уравнение  теплового  баланса получится  в  виде

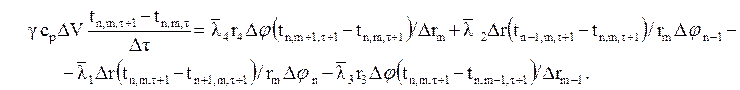
В  данном  случае  уравнение  записано  в  неявной  форме,  для  момента  времени  τ+1.  Система  уравнений  будет  безусловно  устойчива,  но  ее реализация  связана  с  решением  системы  уравнений,  и  если  они  будут  нелинейными,  то  необходимо  использование  процесса  итерации.

Для  сокращения  затрат  машинного  времени  можно  и  в   данном  случае  воспользоваться  методом  расщепления.

3.8.4  Методы  конечных  и граничных  элементов

При  использовании   этих  методов,  как и  в  методе  контрольных  объемов,  исследуемую  область  разбивают  на  одно-,  двух-  или  трех-мерные  элементы.  Но  форма  и  положение  элементов  в  пространстве  произвольны.  Элементы  могут  быть  отрезками  линии,  треугольниками,  четырехугольниками,  октаэдрами,  параллелограммами,  с  прямыми  или  криволинейными  границами.  Обычно  предпочтение  отдают  треуголь-  никам  и  октаэдрам  с  прямыми  границами. Узловые  точки  располагают  в  углах элементов.  Размеры  элементов  и  их  форма  должны  обес-  печивать  наиболее  полную  аппроксимацию  формы  исследуемой плос-  кой  или  объемной  области.  В  местах  резкого  изменения  расчетных  параметров  рассматриваемого  процесса  узлы  сетки  можно  располагать  гуще, то  есть  использовать  неравномерную  сетку,  хотя  решение  в  этом  случае  усложнится.

Второе  отличие  этих  методов  от  конечно-разностных  заключает-ся  в  том,  что  аппроксимируется  не  дифференциальное,  а  интегральное  уравнение. В  методе  конечных  элементов  для  этого  используется  экви- валентность  некоторых  задач теплопроводности  и  конвективного  тепло-массообмена  задачам  отыскания  функций,  обеспечивающих  минимум  неким,  специально  сконструированным  выражениям, называемым  функ- ционалами.  В  методе  граничных  элементов  используются  уравнения  полей,   получаемые  методами   точечных  источников.

Функционалом  от  семейства  функций,  например  типа  f = f(x),  яв-ляется  переменная  величина  Ф = Ф[f(x)],  если  каждой  функции  сово-купности  S  соответствует  некоторое  конкретное  число  Ф.  Простейшим  функционалом является  интеграл  Ф[f(x)]=. Если  вместо  f(x)  под- ставлять  функции,  например  х,  х²,…хⁿ,  то  будут  получаться  числа  ½,  1/3,…1/(n+1).

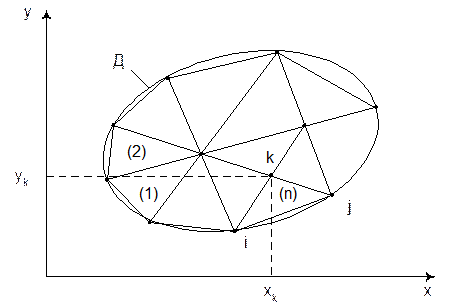
Рисунок 19. – Разбивка области на элементы.

Пример  разбивки двухмерной  области  на   конечные  элементы  показан  на  рисунке  19. Номера  узлов  в  элементе  указывают  в  соответствии  с  движением  против  часовой  стрелки.

Используя  приемы  операционного  исчисления,  можно  показать,  что,  например,  решение  стационарного  уравнения ∂²t⁄∂x²+∂²t⁄∂y²=0  при  граничных  условиях первого  рода  совпадает  с  функцией,  которая  ми-нимизирует функционал . Здесь  t_*(x,y) – фу-нкция  из  допустимого   множества  функций  формы, заданных  в  области  Д. Для  данной  задачи  функции  формы  являются допустимыми, если  они  непрерывны  и  имеют  кусочно-непрерывные  первые произ-  водные.  Кроме  того,  они  должны  удовлетворять  граничным  условиям.

Разбиение  области  и  условия  непрерывности,  накладываемые  на  функции формы,  позволяют  записать  функционал  в  виде  ,  где