Тепломассообмен (физико-математические основы): Учебное пособие, страница 55

Следует  иметь  в виду,  что к  настоящему  времени  разработано  несколько  схем  зонального  метода  расчета  сложного  теплообмена.  Они  отличаются  записью  математических  выражений,  аппроксимирую-щих  процессы  переноса,  последовательностью  и  способами  решения  систем  уравнений.  И  они  непрерывно  совершенствуются.  Поэтому  подробно на  всех  вопросах  мы  останавливаться  не  можем.  Желающим  разобраться  в  тонкостях  зональных  методов  на  первых  порах  рекомен-дуем  изучить  [9,10,11] .

3.11.  Методы  гидро-  и   электротепловой  аналогии

Ранее  было  упомянуто  о  том,  что  аналогичными  являются  процессы,  описываемые  уравнениями,  одинаковыми  по  форме,  по  структуре,  но  разными  по  физическому  смыслу. В  разделе  3.4  данного  пособия  на  основе  подобия  процессов  в подвижных  средах  аналитиче-ски  были  получены  простые  соотношения,  связывающие  параметры  процессов  тепло-  и  массообмена,  гидравлического  трения  и  теплооб-мена.  Но,  оказывается,  на  основе  аналогии  можно  решать  и  более  сложные  задачи тепломассопереноса,  причем экспериментальным  путем,  на  физических  моделях, гидравлических  или  электрических. Устройства,  с  помощью  которых  можно  осуществить  такое  моделирование,  называ-ют,  соответственно,  гидравлическими  или  электрическими  интегратора-ми,  хотя  в  них  используются  конечно-разностные  схемы  по  типу  кон-трольных объемов. Результаты  моделирования  рассчитываются  по  пара- метрам,  измеренным  на  моделях.

Более  точными  и  менее  громоздкими  являются  электроинтегра-торы.  С них  и  начнем  знакомство.  В  них  используются  сетки  типа  сопротивление-сопротивление  и  сопротивление-емкость (R-R  и  R-C  сетки).

Если  моделировать  одномерное  температурное  поле  на  R─C  сетке,  то  схема  модели  будет  выглядеть  как на  рисунке  21.

Пусть  стенка,  площадь  которой  равна F  в  направлении,  перпен-дикулярном  плоскости  рисунка,  разбита  на  N  слоев  толщиной  Δx.  Температура  слоев  в  плоскостях  их  симметрии  равна …,t_n-1,t_n,t_n+1,… Уравнение  теплового  баланса  для  n-го  слоя  стенки  Q_n+1 = Q_n + Q_n-1 по-казывает  равенство  между  приходом  тепла  Q_n+1  и  расходом   его  на  ангрев  n-ого  слоя  Q_n  и  на  отданное  (n – 1)-ому  слою. В  развернутом  виде  это  уравнение  будет  иметь  вид

.

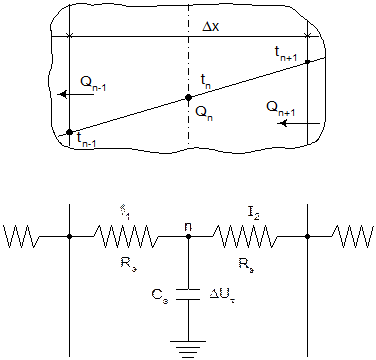
Рисунок  21. – Схема  слоя  стенки  и  его  электромодели

После  преобразования  его  можно  привести  к  виду

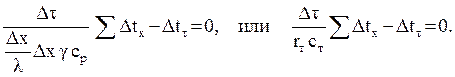                                             (а)

Здесь  r_т= Δx/λ – это  тепловое  сопротивление  слоя;

с_т -  теплоемкость  слоя  на  1м²;

Δt_x – перепад  температур  между  слоями (по  координате);

Δt_τ – изменение  температуры  за  время  Δτ.

Для  точки  n  электрической  схемы  баланс  энергии  запишется  в  виде  I₁ – I₂ = ΔI = c_э ΔU_τ/Δτ΄,  где  ΔU_τ – изменение  напряжения  на  конден-саторе  емкостью  с_э.  Это  уравнение  можно  переписать  в  виде

                                               (б)

Как  видно,  уравнения  (а)  и  (б)  имеют  одинаковую структуру. Ана-логом  перепада  температур Δt  является  перепад  напряжения  ΔU.  Если  коэффициент  пропорциональности  между  ними  равен m_т (масштабу  по  температуре),  то  Δt = m_тΔU, и  уравнение (а)  можно  переписать в  виде

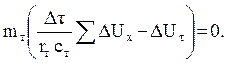
Поскольку  m_т ≠ 0   имеем

                                                                                      (б΄)

Из  равенства  (б)  и  (б΄)  следует  равенство    

Используя  масштабы  по  времени  m_τ = Δτ′∕Δτ, по  сопротивлению m_r=R_э/r_т  и  по   емкости  m_e = c_э/с_т ,  последнее уравнение  можно  переписать  в  виде     

m_τ = m_r m_e.  Если  учесть,  что  Δτ′ = m_τ Δτ,  то  можно  сообразить,  что  уве-личение  m_τ  за  счет  m_r  и  m_e  позволит  быстропротекающий  реальный  процесс  на  модели  растянуть  и  тем  самым облегчить  измерения,  а  слишком  длинный  процесс,  наоборот,  сократить,  чтобы  не  дежурить  сутками  в  процессе  экспериментов.