Тепломассообмен (физико-математические основы): Учебное пособие, страница 39

Интегральное  преобразование    уменьшает  число  независимых  пере-  менных  на  единицу,  причём  в  задачах  для  одномерного  поля  дифференциальное  уравнение  в  частных  производных  переходит  в  обыкновенное  дифференциальное;  а  если  к  таковому  применить  преобразование  ещё  раз,  то  оно  перейдёт  в  алгебраическое  отно-  сительно изображений.  Уравнение  решается  относительно  изображения  искомой  функции  и  переводится  в  оригинал.

Вид  ядра  преобразования  зависит  от  условий  решаемой  задачи.  Так  для  тела  неограниченной  протяженности  удобно  применить  комплексное преобразование Фурье, у которого K(px)= (1/) exp (- ipx).  Интеграл,  соответственно,  берётся  в  пределах  от  - ¥  до +¥.

При  граничных  условиях  первого  рода  удобнее  использовать  синус –  - преобразование  Фурье,  а  при  граничных  условиях  второго  рода -  косинус – преобразование  Фурье. При  этом  ядра  преобразований  имеют  вид  K(px) = × sin (px),   K(px) = ×cos (px);  для  тел   цилиндрической  формы  K(px) = r J(pr),  где  J(pr)  -  функция  Бесселя,  а  r  -  текущий  радиус  цилиндра.  Интеграл  с  таким  корнем  называют  преобразованием  Ханкеля.

В  интегральном  преобразовании  Лапласа  в  качестве  ядра  используется     exp (- pt). 

Обобщенное  интегральное  преобразование  объединяет  конечные  преобразования  Фурье  и  преобразование   Ханкеля.  При  этом  исполь-  зуются  обобщенные  функции  H_z(h) и  N_z(h).  Преобразование  имеет  вид

Методика  решения  уравнений  и  их  систем  заключатся  в  осуществлении  ряда  последовательных  операций.  Например,  для  одномерных  задач  теплопроводности,  зависящих  от  координаты  и  времени,  необходимо

·  на  основе  анализа  дифференциального  уравнения  и  краевых  условий  выбрать  подходящее  ядро  интегрального  преобразования;

·  умножить  дифференциальное  уравнение  и  граничные   условия на  выбранное  ядро  преобразования  и  проинтегрировать  полученные  выражения  в  соответствующих  пределах  по  переменной,  подлежащей  исключению;  в  результате  вместо  системы  дифференциальных  уравнений  в  частных  производных  относительно  оригинала  функции  получим  систему  обыкновенных  дифференциальных  уравнений  для  изображений  функций,  которые  учитывают  начальные (при  преобразовании  Лапласа)  или  граничные (при  преобразовании  Фурье)  условия;

·  решить  обыкновенные  дифференциальные  уравнения  относительно  преобразованных  функций;  если  решение  этих   обыкновенных  дифференциальных  уравнений  невозможно,  то  к  ним  следует  еще   раз  применить  подходящее  интегральное  преобразование  относительно  второй    независимой  переменной,  чтобы  получить  алгебраические  уравнения,  решение  которых  более  просто;

·  решив  задачу  относительно  изображения  искомой  функции,  осуществить  обратное  преобразование,  используя  так  называемые  формулы  обращения,  например,  для  комплексного  преобразования  Фурье      для  синус – преобразования  Фурье    для  преобразования  Лапласа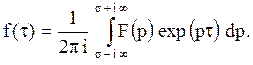 

·  определить  произвольные   постоянные  интегрирования,  содержа-  щиеся  в  решении  уравнения,  используя  краевые  условия  задачи.

В  настоящее  время  в  литературе  имеются  таблицы  прямого  и  об ратного  преобразования  многих  функций,  встречающихся  в  практике  расчётов  по  тепло-  и  массообмену.  Пользуясь  ими  так  же,  как  таблицами  интегралов,  можно,  не  интегрируя функции  с  ядром  для  получения  изображения   и  не  используя  формулы  обращения,    получать  необходимые  решения  в  конечной  форме.  Правда,  иногда  приходится  преобразовывать  выражения  и  уравнения,  чтобы  подогнать  их  под  табличные.

Таблицы  прямого  и  обратного  преобразований  содержат  по  две  колонки,  например,  для  преобразования  Лапласа: