Тепломассообмен (физико-математические основы): Учебное пособие, страница 52

Подстановкой  выражений  для  f_iν  и   J_iν  в  уравнения  и  умножением  на  π  приведем  их  к виду

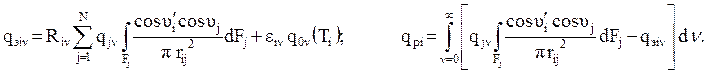
Выражение 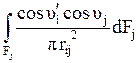   есть локальный диффузный  угловой  коэф-фициент  с  площадки  dF_i  на  поверхность  F_j,  то  есть  φ(dF_i, F_j).  При  ин-тегрировании  уравнений  по  F_i  все  величины,  кроме  углового  коэффици-ента,  будут  постоянными,  а  будет  представлять  сред-ний  диффузный  угловой  коэффициент.  Теперь

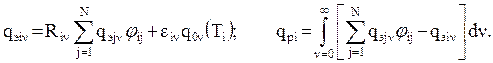
Чтобы  от  плотностей  тепловых  потоков  q  перейти  к  просто  пото-кам  Q=qF,  умножим  обе  части  уравнений  на  F_i.  Тогда  получим

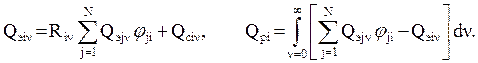
Здесь  q_эiν F_i φ_ij=q_эiν F_j φ_ji  по  свойству  взаимности.

При  учете  зависимости  радиационных  свойств  от  частоты  излуче-ния  прибегают  к  упрощению,  разбивая  весь  спектр  излучения  на  k  полос,  в  пределах  которых  радиационные  свойства  принимают  постоянными,  равными  средним  по  полосе.  Тогда

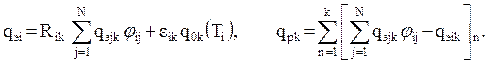
Если  радиационные  свойства  поверхностей  можно  принять  не  зави-сящими  от частоты  ν,  то

Исключив  из  этих  уравнений  эффективные  потоки,  можно  полу-чить  одно  уравнение  в  виде

а  при  небольшом  количестве  поверхностей  можно  составить систему  уравнений  и  решить  ее  совместно  аналитическим  путем.  Но  уже для  сис-темы  из  трех  тел  формулы  получаются  непростыми.  Так  для  замкнутой  системы  из двух  вогнутых  поверхностей,  заполненной "серой"  средой  со  степенью  черноты  ε_с,  расчетная  формула  в  развернутом  виде  получается  довольно  громоздкой:

Здесь  Θ = (T/100)⁴,  C₀ = 5,67 Вт/м² К⁴.

Правда,  эту  формулу  можно  записать  в  сокращенном  виде,  если  обозначить

.

Тогда  q_p2 = C₀ε_пр(Θ₁ – Θ₂).  Величину  ε_пр  называют приведенной степенью  черноты  системы  тел, а  произведение  С₀ε_пр= С_пр называют  приведенным  коэффициентом  излучения  системы  тел.

3.9.1.  Классический  и  резольвентный  зональные  методы

Разница  между  первым  и  вторым заключается в  том,  что  в  клас- сическом  методе,  как  и  в  предыдущих  выводах,  используются  эф-фективные  потоки,  которые  являются  промежуточными  звеньями  меж-ду  результирующими  и  собственными  потоками.  Но  в  предыдущие  уравнения  входит средний  геометрический  угловой  коэффициент,  а  в  классическом используются обобщенные средние,  в  резольвентном –обобщенные  разрешающие.

Постановка  задач  в  общем  случае  может  быть  разная:

1)  заданы  температуры  всех  поверхностных  и  объемных  зон,  требуется  найти  результирующие  потоки.  Такие  зоны  называют  зонами  I- ого  рода;

2)  заданы  результирующие  потоки  для  всех  поверхностных  и  объемных  зон,  требуется  найти  температуры.  Такие  зоны  называют  зонами  II-ого  рода;

2)  для  части  зон  заданы  температуры,  а  для  остальных – результирующие  потоки. Такую  постановку  задач  называют  смешанной.

В классическом методе исходным является уравнение Q_p= Q_пг - Q_c= Q_п- Q_э,  в  котором  Q_p – результирующий  лучистый  поток;

Q_пг – поглощенный   поток;

Q_c – собственный    поток;

Q_п – падающий  поток;

Q_э – эффективный  лучистый  поток.

Падающий  лучистый  поток в  классическом  методе  выражается  через  эффективный,  но  умноженный  на  средний  обобщенный  угло- вой  коэффициент 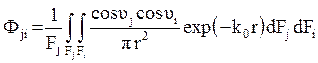   ( для  зон  F_j и  F_i ), учитывающий способность среды пропускать излучение  за счет  введения в формулу коэффициента пропускания среды D_c= 1 – A_c = 1 – 1 + exp(- k₀r).

Поэтому  (при общем количестве зон  n₁ + n₂ + m₁ + m₂ = N + M)       Q_эi=-для поверхностных зон I-ого рода(i=1,…,n₁);

Q_эi =  - для  поверхностных зон  II-ого  рода(i=n+1,…,N);

Q_эi = Q_ci,  где   i = N+1,…,N+m₁, для  объемных  зон  I-ого  рода;

Q_эi = A_ci - для  объемных  зон  II-ого  рода (i=N+m₁+1,…, N+M).

Решая  систему  этих  уравнений,  находят  Q_эi  для всех  зон,  а  затем  находят 

Q_pi =  -   для  поверхностных  зон  I-ого  рода;