Тепломассообмен (физико-математические основы): Учебное пособие, страница 24

в  котором   а = l / g с_р – температуропроводность  среды,  характеризующая  теплоинерционные  свойства  тела  и  являющаяся  мерой  скорости  выравнивания  температуры  в  нем.  Скорость  распространения  тепловой  волны  в  теле  w_t = 2,  где   - частота  колебаний  температуры.

Левая  часть  этого  уравнения   является  субстанциональной  производной,  состоящей  из  локального  (¶t/¶t)  и  конвективного   изменения[ w_x (¶ t/¶ x) + w_y (¶ t/¶y) + w_z (¶ t/¶z) ]  температуры.  В  таком  виде  она  используется  для  описания  конвективного  теплообмена.  В  твёрдых  телах  w_x = w_y = w_z = 0,  поэтому  в  левой  части  остаётся  только  локальное    изменение  температуры.

Уравнение  в  виде

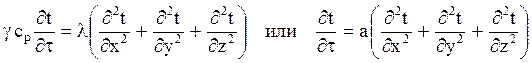
называется  уравнением  теплопроводности  в  твёрдом  теле при а = const.

Если  изменение  температуры  происходит  только  в  одном  направлении,  например,  по  оси   х,  совпадающей  с  толщиной  бесконечной  пластины,  с  радиусом  бесконечно  длинного  цилиндра  и  с  радиусом  шара  (одномерное  поле  температур),  то  уравнение  теплопроводности  можно  записать  в  обобщенном  виде

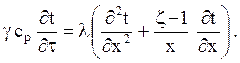
Здесь   z – коэффициент  формы  тела,  численные  значения  которого     даны  в  1.1.            

Приведенные  уравнения  переноса  получены  при  условии  постоянства  l, g  и  с_р,  а  также  при  отсутствии  источников  или  стоков  тепла  в  объёме  тела. 

При  переменном   l  производные  правой  части  следует  записывать  в  виде   ¶(l ¶t/¶x)/¶x,  а  при  наличии  стоков  или  источников  тепла  к  правой  части  добавить  еще  один  член  в  виде  ±q_V ,  представляющий  объёмную  мощность (Вт/м³).

При  стационарном  режиме  (¶t/¶t) = 0,  и  уравнение теплопро-  водности   для  одномерного  поля  приобретает  вид

Решение  этого  уравнения  несложно  и  может  быть  получено  простым  его  интегрированием  по  двум  переменным.

2.5.  Уравнение  переноса  массы

Вывод  этого  уравнения,  как  и  уравнения  неразрывности,  базируется  на  законе     сохранения  массы  материи.

    Согласно  первому  закону  Фика  в  объём  dV = dl_xdl_ydl_z через  левую  грань  dl_ydl_z   за  счёт  молекулярной  диффузии  поступает  поток  вещества  с  концентрацией  С₀           

а  через  противоположную   такую  же  грань   выходит  поток

Приращение  потока  среды  в  объёме  dV  по  оси  х

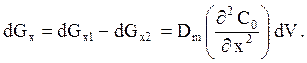
Полное  приращение  по  всем  трем  осям

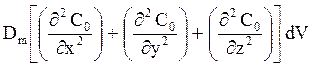
идёт на  изменение  концентрации  во  времени  и  может  быть  представлено  как  (¶С₀ /¶t) dV,  если  диффузия  молекулярная,  то  есть  dV  неподвижен.   Приравнивая   два  этих  выражения,  получим  дифференциальное  уравнение молекулярной  диффузии

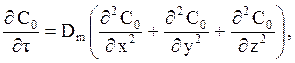
которое  называют  вторым  законом   Фика.

Следует  иметь  в  виду,  что  оба  приведенных  закона  Фика  справедливы  только  для  бинарных  смесей.  Диффузионный  перенос  в  многокомпонентных  смесях  намного  сложнее.

При  конвективной  диффузии  изменение  концентрации  компонента  в  объёме  dV  будет  описываться  зависимостью  dG = =(dС₀/dt) dV,  в  которой  субстанциональная  производная

(dС₀ /dt) = (¶С₀ /¶t) + w_x(¶С₀ /¶x) + w_y(¶С₀ /¶y) + w_z(¶С₀ /¶z) .

Это  уже  будет  конвективная  диффузия.

При  наличии  термо-  и  бародиффузии  в  правой  части  уравнения  появятся  соответствующие  слагаемые.

2.6.    Уравнения   теплоотдачи

На  границе  твёрдого  тела  с  окружающей  средой,  то  есть  на  его  поверхности,  соблюдается  равенство  плотностей  тепловых  потоков  -   входящего  и  выходящего.  Окружающая  среда  может  быть  и  твёрдым  телом,  контактирующим  с  рассматриваемым.

Если   окружающая  среда  подвижна,  то  на  поверхности  тела  будет  конвективный  теплообмен  и  тогда  a (t _п -  t _c ) = -  l (¶t/¶n)_п ;  если  же  окружающая  среда  неподвижна,  то  l ₁(¶t₁/¶n)_пн = l ₂(¶t₂/¶n)_пв.   Здесь  индекс  «пн»  означает  что  градиент  температуры  взят  у   поверхности  тела,  с  наружной  стороны,  а  индекс  «пв»  -  что  он  взят  у  поверхности  же ,  но  с  внутренней  стороны;  t _п   и   t _c ,соответственно,  температуры   поверхности  тела  и  окружающей  среды.