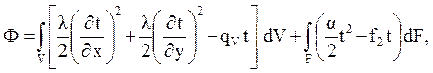
минимизируемый на распределениях температуры, удовлетворяющих граничным условиям tп = f1 и имеющих кусочно-непрерывные производ-ные по пространственным координатам х и у.
Если сетка состоит из М конечных
элементов, при построении которых в качестве узловых параметров
используются лишь значения функций, то, как было указано ранее, можно
написать ![]() А вклад элемента с
номером n составит
А вклад элемента с
номером n составит
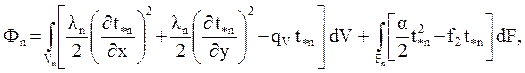
причем второй интеграл в этом уравнении отличен от нуля только при условии, что граница Fn данного конечного элемента принадле- жит границе объема V, на которой определены граничные условия.
3.9 Методы решения уравнений лучистого теплообмена
Лучистый теплообмен в системе тел является процессом весьма сложным. Если для собственного излучения поверхностей твердых и жид-ких тел свойства окружающей среды безразличны, то для теплообмена между этими поверхностями свойства среды имеют первостепенное зна-чение и определяют сложность расчетов, так как наличие поглощения, собственного излучения и рассеяния усложняет структуру уравнений и приводит к появлению дополнительных трудноопределимых величин.
Чтобы получить поверхностные плотности лучистых потоков, как видно из 2.1, нужно осуществить интегрирование уравнений по частоте излучения и по пространственному углу. Кроме того, нужно знать ин-дикатрисы отражения и рассеяния.
В случае непрерывного спектра излучения интегрирование по час-тоте несложно, а при селективном любая попытка бесполезна, так как описать спектр излучения никакой функцией невозможно. К этому добавляются сложности определения индикатрис отражения и рассеяния, которые зависят от многих трудно учитываемых и нечетко оцениваемых факторов. Поэтому имеющиеся к настоящему времени аналитические решения уравнений переноса излучения практического значения не имеют. В учебной литературе аналитические решения есть, в том числе и для систем, состоящих из любого числа поверхностей, при задании любых условий на них. Но получены они в предположении "серого" излучения как твердых поверхностей, так и окружающей газовой среды.
Наиболее точные решения задач лучистого теплообмена, в том числе с учетом селективности, в системах сложной геометрической фор-мы дают зональные методы.
Суть этих методов, как и предыдущих, заключается в разбиении поверхностей и объёмов на расчётные зоны. Степень разбивки как поверхностей, так и объёмов зависит от их геометрии, от равномерности распределения температур, от степени точности расчётов, а также от возможностей вычислительной техники.
Сложность расчетов определяется количеством зон, способностью среды поглощать, рассеивать и излучать тепловую энергию, особенно при учёте селективности газов. В несложных системах возможно решение приведенных в 2.1 уравнений переноса излучения между поверхностями даже с селективно излучающей средой.
Пусть, например, система состоит из N зон, у каждой из которых радиационные свойства, температура и интенсивность эффективного из-лучения постоянны и не зависят от направления. Иначе говоря, поверх-ности излучают и отражают диффузно.
Через dFi и dFj обозначим элементарные площадки на поверхностях зон, соответственно, Fi и Fj, а через rij расстояние между площадками. Тогда уравнения переноса применительно к площадке dFi и монохрома-тическому излучению запишутся следующим образом:
интенсивность потока эффективного излучения с частотой ν
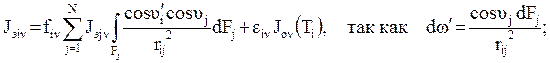
плотность интегрального результирующего потока
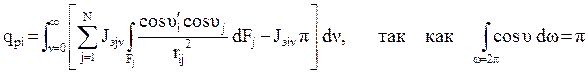 .
.
Для диффузных поверхностей индикатриса отражения fiν = Riν/π, интенсивность излучения Jiνqiν/π. Здесь Riν – полусферическая отражательная способность.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.