Тепломассообмен (физико-математические основы): Учебное пособие, страница 19

В  первом  случае  перенос  излучения  происходит  между  поверх-ностями  тел,  ограничивающих  объем  лучепрозрачного  газа.  Схема  лу-чистых  потоков  относительно  элементарной  площадки  dF  на  поверхности  твердого  тела  показана  на  рисунке  9. 

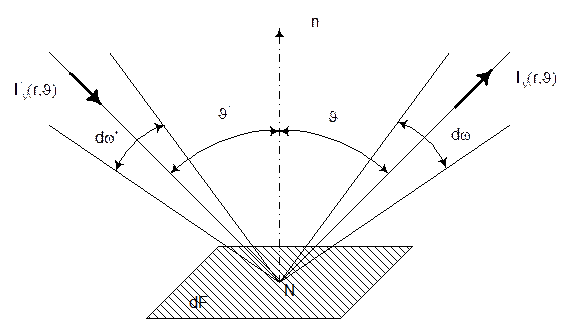
Рисунок 9. – Схема лучистых потоков на площадке dF

Для  общности  радиационные  свойства  поверхностей,  образующих  систему,  примем  зависящими  от  координат,  а  также  от  направления  лучистого  потока  и  от   частоты  излучения;  распределение  температу-ры  по  поверхности  - произвольное.

Уравнения  переноса  могут  быть  получены  из  уравнения  энерге-тического  баланса  лучистых  потоков.

Спектральная  интенсивность  эффективного  излучения  J_ν,  по-кидающего  элементарную  площадку  в  некотором  направлении  ,  рав-на  сумме интенсивностей  собственного  и  отраженного  потоков  и  может  быть  записана  в  виде

, где   - спектральная  плотность  потока  излучения  абсолютно  черного  тела;

ν – частота  излучения;

Т(r,N)  -  температура  поверхности  в  точке  N;

ε_ν – направленная  степень  черноты  поверхности;

 - индикатриса  отражения,  то  есть  функция  распределения  отраженного  излучения  по  полупространству.

Плотность  потока  результирующего  излучения  может  быть  определена  как  разность  между  поглощенной  и  собственной  плотностями  потоков  излучения,  или  как  разница  между  падающей  и  эффективной  плотностями.  По  второму  варианту

.

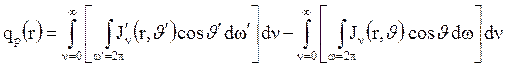Здесь  в  качестве  граничных  условий  могут  быть  заданы  температуры  поверхностей (задачи  первого  рода)  или результирующие  потоки (задачи  второго рода).  В  первом  случае  определению  подлежат  плотности  результирующих  тепловых потоков,  а  во  втором – темпера-туры  поверхностей.  Но  в  реальных  схемах  чаще  бывают  смешанные  задачи.

В  частично  прозрачных  средах  излучение  ограничивающих  по-верхностей,  проходящее  через  нее,  поглощается   пропорционально  ее  коэффициенту  поглощения.  В  то  же  время  такая  среда  испускает  и  собственное  излучение.  В  газо-пылевом  потоке  к  тому  же  происходит  рассеяние  лучистой  энергии.

Рассмотрим  перенос  энергии  излучением  в  среде,  только  поглощающей (условно  не  рассеивающей  и  не  имеющей  собственного  излучения).  При  этом  будем  считать, что  среда  однородна  на  всем  пути  луча,  то  есть  степень  ослабления  потока  излучения  везде  одинакова.  В  этом  случае  изменение  величины  лучистого  потока  должно  быть  пропорционально его  пути  в  среде и  значению  его  величины  на  входе  в  среду,  то  есть

dQ = - k₀ Q dx .                                                                                     Здесь  k₀ – коэффициент  пропорциональности, называемый коэффициен-том   ослабления   луча;

Разделяя  переменные  x  и  Q   и  интегрируя  полученное  уравнение  по длине  луча от 0 до  z, получим  ln (Q_к / Q_н ) = - k₀ z  или Q_к /Q_н = exp(- k₀ z).

Вычитая  из  единицы  левую  и  правую  части  последнего  равенства,  после  приведения  левой  части  к  общему  знаменателю,  получим  (Q_н – Q_к)/Q_н =  1 – exp ( - k₀ z).  Разница  в  скобках  -  это  погло-  щенная  часть потока  на  отрезке  пути  z,  а  отношение  части  к  целому  Q_н  есть коэффициент  поглощения 

А = 1  -  exp( - k₀ z).

Это  выражение  называют    законом  Бугера,  а  произведение  k₀ z -  -оптической  толщиной  слоя.

Строго  говоря,  закон  Бугера  справедлив  лишь  для  монохроматического  излучения,  но  его  можно,  с  некоторыми  добавле-  ниями, использовать для определения  А  и  при  интегральном  излучении.

Логика  подсказывает,  что  поглощательная   способность   газов  должна  расти  с  увеличением  давления  и  уменьшаться  с  ростом  температуры,  так  как  от  них  зависит  количество  молекул  в  единице  объёма.  Должна влиять  и  концентрация  поглощающих  компонентов  в  смеси.  Эти  зависимости  можно  учесть  в коэффициенте  ослабления.