Тепломассообмен (физико-математические основы): Учебное пособие, страница 22

Подробный  вывод   уравнения  движения  вязкой  сжимаемой  среды  сложен  и  громоздок,  особенно  в  случае  переменных  физических  свойств  её.  Поэтому  упростим  вывод,  принимая потери на рассеяние энергии равными  нулю,  среду  несжимаемой,   а  движение  её  -  одномерным.  Тогда  на  объём  dV  в  направлении,  например  оси  x,  будут  действовать    сила  тяжести   dF₁ = g_x g dV,  равнодействующая  силы  давления  окружающей  среды  dF₂ = - (¶P/¶x) dV  и  сила  внутреннего  трения, обусловленная  вязкостью  среды

dF₃ = .                                    Здесь   g _x  -  проекция  ускорения  свободного  движения  на  ось  x;

m = n g - динамическая  вязкость  среды;

n - кинематическая    вязкость  среды.

Знак  минус  перед  (¶Р/¶x)  поставлен  потому,  что  ускорение  положительно  в  направлении  падения  давления,  а   вектор  (¶Р/¶x)  положителен  в  направлении  роста  давления.

Структура  первых  двух   формул понятна  без  особых  пояснений,  а  вывод  выражения  для  равнодействующей  силы  трения  поясним  на  примере  плоскрго  двухмерного  течения (рисунок 12).                                                                                                           Сила  трения,  вследствие

                   y              dl _y                                              неравномерности   скорости,  воз                                                                        никает  на  боковых  гранях  вы   x                                                                  деленного  элемента  среды. Она 

                                                                      пропорциональна  их   величине.

  dl _x             S                       S + (¶ S/¶y)dl _y  На  левой  грани  сила  трения, препятствующая  движению  эле- мента,  направлена  против  его

w_x                                    движения  и  равна  S dl_x dl_z.  На правой  грани  скорость  среды больше,  чем  в самом  элементе,

Рисунок  12 . – Схема  сил  трения.             поэтому сила трения  направлена                                                                                   в  сторону  его  движения. Равно-действующая этих  сил  dF  по  оси  x  равна  разности  [S + (¶S/¶y) dl_y] dl_x dl_z - -S dl_x dl_z = (¶S/¶y) dV.  По  Ньютону  напряжение  трения  на  границе  слоёв  S = m (¶w_x/¶y),  поэтому  равнодействующая 

С  учётом  трехмерности    скоростного  поля 

dF₃ =

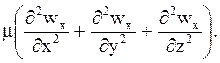
Используя  приведенные  выражения  для  действующих  сил,  математическое  выражение  второго  закона  Ньютона  получим  в  виде 

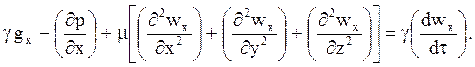
В этом уравнении  dw_x /dt - так  называемая  субстанциональная   (полная)  производная,  то  есть  связанная  с  перемещением  субстанции  в  пространстве.

Проекция  скорости   w_x  в  общем  случае  является  функцией  координат  и  времени,  поэтому  её  полная  производная

Приращение  координаты  точки,  отнесенное  к  отрезку  времени,  есть  проекция   скорости  этой  точки  на  ось  координат,  поэтому   окончательно  уравнение  движения  среды  относительно  оси  x  выглядит  следующим  образом:

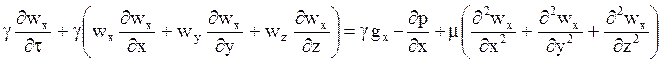
Уравнение  движения  относительно  оси  у  получается  аналогично:

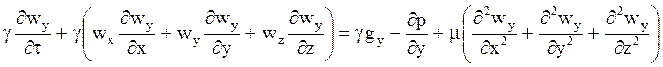
Таким  же образом  записывается   уравнение  относительно  оси   z .

Используя  формулы  связи  для  осей  координат,  можно,  как  и  в  случае  уравнения  сплошности,  уравнения  движения  получить  в  цилиндрических  или  в  сферических  координатах.  Но  перевод  этот  очень  громоздок,  и  здесь  не  приводится.  При  необходимости  лучше  воспользоваться  справочной  литературой.

Для  сжимаемых  газов  такие  уравнения  даже  в  окончательном  виде  очень  громоздки  и  здесь  также  не  приводятся.

Предыдущие  уравнения  получены  для  движения,  происходящего  под  действием  статического  давления  р (вынужденного  движения).  Но  движение  на  макроуровне  может  происходить  и  под  действием  силы  тяжести,  то  есть  из-за  разницы   плотностей  вследствие  наличия  разности  температур (свободное  движение).  В  этом  случае  изменением  плотности  пренебрегать  нельзя,  и  уравнение  движения  следует  записывать  в  виде