1 (110,0) 53,7 32,5 23,8 (60,0)
(110,0) 75,2 42,5 27,3 (60,0)
2 (140 0) 71,2 38,8 46,3 (100,0) (140 0) 78,3 68,7 99,2 (100,0)
3 (170 0) 89,4 58,8 69,4 (140,0) (170,0) 156,6 128,8 54,6 (140 0)
4 (200,0) 114,4 79,4 99,4 (180,0)
(200,0) 134,9 59,4 239,9 (180,0)
В таблице жирно подчёркнуты начальные значения температуры, а в скобки взяты граничные значения.
Из таблицы видно, что во втором случае (справа) начальное распределение температур (Dt = 0) и изменение температур поверхностей (n = 1, n = 5) одинаково с первым (слева). Но в первом варианте в точ ках 2, 3, 4 значения температуры меняются плавно, а во втором варианте их значения то резко увеличиваются, то резко уменьшаются. Эти колебания объясняются не ошибками округления, а внутренними свойствами схемы расчёта, не проявляющимися только при определенных условиях, а именно при значениях DFon меньше определенного значения. В частности, при l = const устойчивое решение по явной схеме получается при DFo £ 0,5. Но следует иметь в виду, что это ограничение справедливо полностью только для пластины с граничными условиями первого рода. О других граничных условиях – нес- колько позже.
При использовании безусловно устойчивой явной схемы для решения получающейся системы уравнений применяется метод прогонки, являющийся частным случаем метода исключения Гаусса. Суть его заключается в расчёте вспомогательных величин, позволяющих определять входящие в уравнения температуры, используя предположение о её линейном изменении на отрезке Dx.
При постоянных l, g и ср уравнение температур по неявной схеме запишется так: t n ,t (1 + 2 DFo n) = t n + DFo n(t n+1,t + t n-1,t). В нём три неизвестных температуры. Для сокращения записи представим это уравнение в виде -An t n+1,t + Bn t n,t - Cn t n-1,t = Dn , где An = Cn = DFo n , Bn = 1 + 2DFo n , Dn = t n.
Учитывая предположение о
линейности изменения t на отрезке Dх, примем t n-1,t = E n-1 + Fn-1 t n,t и подставим в
предыдущее уравнение. Из него найдём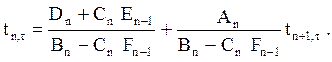 
Учитывая то же предположение о линейности, запишем t n,t = E n + + Fn t n+1,t . Сравнивая это выражение для t n,t c предыдущим, видим, что E n = (Dn + Cn Fn-1)/(Bn – Cn Fn-1); Fn = An/ (Bn – Cn Fn-1).
По этим формулам можно рассчитать коэффициенты E n и Fn для всех n точек по толщине пластины, а температуры - по формуле t n,t = = E n + Fn t n+1,t ,в обратном порядке.
При выполнении первого шага по времени значения исходных температур берутся из начальных условий, а при последующих шагах – с предыдущего решения.
Если уравнение в неявной форме записано с учётом зависимости l, g и ср от температуры, или от координаты в неоднородных телах, то методом прогонки также можно пользоваться, но на каждом временном шаге необходимо организовать процесс итерации. При этом можно использовать и простой метод, принимая значения g, l, ср с предыдущего решения в качестве первого приближения, а можно использовать и метод Ньютона.
Мы рассмотрели две схемы построения конечно-разностных уравнений, или, как говорят, по двум шаблонам, которые можно изобразить следующим образом:
t n,t t n-1,t t n,t t n+1,t
♠ ·
ª ·
•
• • •
t n-1 t n t n+1 t n
шаблон явной схемы шаблон неявной схемы.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.