Тепломассообмен (физико-математические основы): Учебное пособие, страница 27

В  левой  части  уравнения  движения  относительно  оси  х    порядок  П[w_x(¶w_x/¶x)] =1×1:1=1,  П[w_y(¶w_y/¶y)] =d×1/d=1;  влиянием  силы  тяжести  в  пограничном  слое  можно  пренебречь;  давление,  понятно,  должно  быть  достаточно  большим,  поэтому  примем  П(¶p/¶x) =1;  в  правой  части,  в  скобках,  П(¶ ²w_x/¶x²) =1,  а   П(¶ ²w_x/¶y²) =1/d² ,  то  есть  намного  больше  первого,  поэтому  ¶²w_x/¶x²  можно  отбросить.  Порядок  оставшихся  членов  правой  части,  очевидно,  должен  соответствовать  порядку  членов  левой  части.  Если  принять  П[m(¶ ²w_x/¶y²)] =1,   то    П(m) =d²  и  порядок  всех  конвективных  членов  уравнения  движения  относительно  оси  y    не  больше  d.  Значит  от  этого  уравнения,  если  также  пренебречь  силой  тяжести,  останется  только  (¶р/¶у) = 0.  Это  равенство  можно  доказать  и  более  строго.

Если  для  t  принять  П(t) = 1,  то  в  левой  части  уравнения  переноса  энергии  оба  члена  в  скобках  будут  иметь  порядок    единицы.  А  в  скобках  правой  части  П(¶ ²t/¶y²)>>П(¶ ²t/¶x²),  поэтому  можно  оставить  лишь  второе  слагаемое.

После  упрощений  получается  следующая  система  уравнений:

.

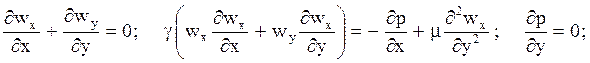
Интегрировать  эту  систему    уже  проще.  Для  турбулентного  пограничного  слоя    она  немного  сложнее,  но  только  за  счёт   коэффициентов  переноса  m _т   и  l _т, как  и  в  уравнениях  для  потока:

Здесь,  как  и  в  предыдущих  случаях,  пренебрежимо  малыми  считаются  градиенты  давления  и  пульсаций  по  оси  х.

Следует  иметь  в  виду,  что  применение  теории  пограничного  слоя  ограничивается  большими  числами  Рейнольдса,  то  есть  большими  скоростями  среды  и  малой  её  вязкостью.

2.9.  Условия  однозначности

Уравнения  тепло-  и  массоперноса   выводятся  в  предположении  бесконечно  малого  объёма  среды  и  справедливы  в  любом  случае,  но  они  не  отражают  развития  процессов  во  времени,  во всём  объёме  тела,  в  зависимости  от  внешних  условий .  А  процессы,  особенно  теплообмена,  нельзя  полностью  изолировать  от  внешних  воздействий .

Чтобы  из  бесчисленного  множества  задач,  решаемых  с  помощью   дифференциальных  уравнений,  выделить  определенную  группу  их,  необходимо  к  решаемому  уравнению,  или  к  системе   уравнений,  добавить  условия,  уточняющие  физическую  сущность  задач,  то  есть,  как  говорят,  нужно  поставить  задачу.  Эти  дополнительные  условия  называют   условиями  однозначности.  В  них  входят  геометрические,  физические,  временные  и  граничные  условия.

Геометрические  условия  определяют  форму  твёрдого  тела  или  потока  подвижной  среды.  Они  учитываются   записью  уравнений  в  соответствующей  системе  координат.

Физические  условия  определяют  значения  или  зависимости  физических  свойств  тела  или  среды  от  параметров  их  состояния.  Они  учитываются  или  постоянными   числами,  или  определенными  формулами.

Временне  условия  определяют  особенности  протекания  процессов  во  времени,  изменения  вспомогательных  величин,  таких  как  коэффициент  теплоотдачи  при  нагреве  тела  или  коэффициент  гидравлического   трения. Кроме  того,  в  эти  условия  входят  начальные  условия  в  виде  уравнений  начального  распределения  температур,  скоростей,  давлений  и  других   параметров.  Учитываются  временне  условия  записью  соответствующих  формул  и  уравнений.

Граничные  условия  определяют  взаимодействие  рассматриваемого  тела  или  объёма  с  окружающей  средой,  с  окружающими  телами.

Гидродинамические   граничные  условия  обычно  несложны,  потому  что  составляющая  скорости  потока, касательная  к  поверхности  твёрдого  тела, равна  нулю (сказывается  эффект  «прилипания»  газа  или  жидкости  к  поверхности  твёрдого  тела),  а  температура   потока  и  поверхности  одинаковы. Усложняются  они  при  организации  вдува  или  отсоса  части  потока  через  поверхность  канала,  или  при  наличии  реакций  на  поверхностях.