Тепломассообмен (физико-математические основы): Учебное пособие, страница 36

Добавим  к  уравнению  условия  однозначности:  а = (λ /γ с_р) = const;    α(τ) = const;  t(x,0) = t_н = const;  ()_x=0 = 0  при  τ > 0;  α(t_п – t_с) = -.

Здесь  t_п – температура  поверхности  пластины  при  τ > 0.

Приведем  уравнение  к  безразмерному  виду,  принимая  x = sX,  t = t_c - - Θ(t_c – t_н),  тогда  при  х = 0   Х = 0  и  (=0;  при  х = s  t_п = t_c – Θ_п(t_c- t_н),

Θ_п = - Bi Θ_п.  Здесь  Bi – критерий  Био.

Тогда  уравнение  теплопроводности  в безразмерных  величинах  будет  иметь  вид

.

Примем,  что  функция  Q  равна  произведению  двух  функций,  одна  из  которых  - Q_х  зависит  только  от  Х,  а  вторая - Q_t  зависит  только  от  числа  Фурье  Fo.  Учитывая  это,  подставим  произведение   Q_хQ_t  в  уравнение  теплопроводности  и,  поделив  левую  и  правую  части  на  Q_хQ_t,  получим  уравнение  с  разделенными  переменными

¶Q_t/ Q_t ¶ Fo = ¶ ²Q_x / Q_x ¶C².

При  независимости  переменных  Х  и  Fo  полученное  равенство  сохранится  только  тогда,  когда  обе  его  части  будут  равны  какой – то  константе,  например  (-h²).  С  учётом  этого  можно  написать  два  обыкновенных  дифференциальных  уравнения:

¶Q_t/Q_t = - h² ¶Fo,       ¶²Q_х /¶C² = - h² Q_х .

Первое  уравнение   интегрируется  просто,   потенцирование  интеграла  даёт

Q_t = C₁ exp(-h² Fo).

Во  втором  уравнении  функция  должна  быть  такой,  чтобы  её  вторая  производная  была  равна  ей  самой,  умноженной  на  (-h²).  Таких  функций  две  -  sin(hC)  и   cos(hC),  то  есть  частными  решениями  второго урав-  нения  являются  две  эти  функции.  А  согласно  принципу  суперпозиции (наложения)  общее   решение  равно  сумме  частных,  поэтому 

Q_х =C₂ sin(hC) + C₃ cos(hC), а Q =Q_хQ_t=[A sin(hC) + B cos(hC)] exp-(h²Fo)

Производная  от  второго  уравнения

¶Q/¶C = [A cos(hC) - B sin(hC)] h exp(-h² Fo).

Используя  условие  симметричности  температурного  поля  (¶Q/¶C)_C=0 = 0,  получаем  А = 0.  Значит Q = B cos(hC) exp(-h²Fo). Её  производная  ¶Q/¶C= = -Bh sin(hC) exp(-h²Fo). При  х = s,   или  Х =1,  относительная  темпе-  ратура  поверхности  Q_п = B cos(h×1) exp(-h²Fo)  производная  .

Из  граничного  условия   (¶Q/¶C)_C=1= - Bi Q_п    и  вышеприведенной  производной  при  Х = 1  получаем  Q_п = (B/Вi) h sin(h×1) exp(-h²Fo),  а из  равенства  двух  выражений  для  Q_п  получим  соотношение Bi cosh = h sinh ,  или  (cos h / sin h) = h/Bi.  Это  уравнение  называется  характеристическим; его  можно  решить  графическим  способом,  находя  точки  пересечения  прямой  y₁ = h / Bi  с  котангенсоидами  y₂ = ctg h.  Котангенс  -  это   периодическая  функция  с периодом  Т = p ,  область  определения  которой  имеет  бесконечное  число  открытых  интервалов  (p/2) + np ,  где   n = 0…¥ .  Следовательно,  прямая  у₁  будет  пересекать  котангенсоиды  бесконечное  число  раз;  бесконечным  будет  и  количество  корней  характеристического  уравнения  h,  которые  называются  собственными  числами  задачи  (таблицы  корней  характеристического  уравнения  имеются  в  справоч-  никах).   

Характеристическое  уравнение  в этом  случае  можно  записать  как  ctg h _n = h _n / Bi . Каждому значению  h_n  будет  соответствовать  своё  частное  распределение  температуры: 

Q₁ = B₁ exp(-h₁²Fo) cos(h₁ C);     Q₂ = B₂ exp(-h₂²Fo) cos(h ₂ C); . . . .

Общее  решение  дифференциального  уравнения,  как  уже  было  сказано,  определяется  как  сумма  частных  решений:

Для  определения  В_n  запишем  это  уравнение  при  t = 0,  тогда

Q_н = ( t _с – t _н)/ (t _с – t _н) =1  и  1 =    Умножим  обе  части  этого  равенства  на  cos(h _m X) dx  и  воспользуемся  ортогональностью  функций синуса   и  косинуса,  которая  заключается  в  том,  что

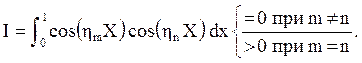
Тогда  в  правой  части  останется  один  интеграл  из  всей  суммы:

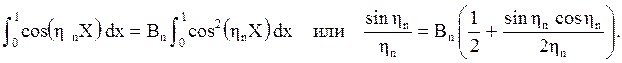
Отсюда

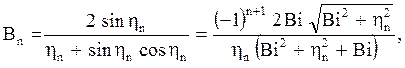
а уравнение температурного поля получится в виде