Тепломассообмен (физико-математические основы): Учебное пособие, страница 26

Рассмотрим  уравнения  движения  и  теплопереноса  для  двухмерного  поля  при  стационарном  режиме    и  постоянных  теплофизических  свойствах  среды:

,

,

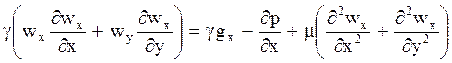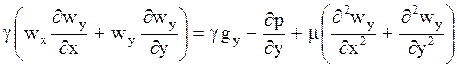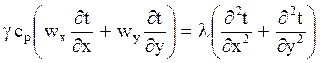
В  уравнениях  движения  сумму  в  левой  части  удобнее  представить в  виде  (¶w_x²/¶x) + [¶(w_xw_y)/¶y],  учитывая  уравнение  неразрывности  потока  (¶w_x/¶x) + (¶w_y/¶y) = 0.  Осуществив  осреднение  в  предыдущих  скобках  и  снова  учтя  уравнение  неразрывности,  но  теперь  в  виде (¶¶x) + (¶/¶y) = 0,  получим  в  левой  части  выражение

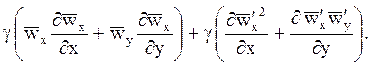
Пренебрегая    силой  тяжести  при  турбулентном  режиме,  осредняя  величины  правой  части  и  перенося  вторую  скобку  из  левой  части  в  правую,  получим  уравнения  движения

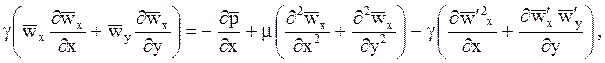
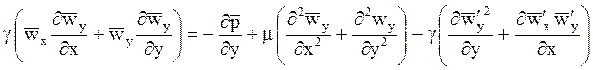
и  уравнение  переноса  энергии

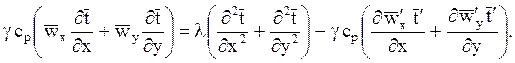
          Вторые  производные  скоростей  и  температуры, а также производные  их  пульсаций  по  оси  х  невелики  и  могут  быть  приняты  равными  нулю.  В  уравнениях  движения  к  молекулярному  трению  добавляется  турбулентное,  поэтому  в  первом  уравнении  - g   заменим  через   m_т (¶_x/¶y) ,  а  во  втором -- g  заменим  через   m_т(¶/¶y), где  m_т – турбулентная  динамическая  вязкость.  В  уравнении же  переноса  энергии  выражение  gс_р,  как  уже  известно,  представляет  конвективную  часть  теплового  потока,  поэтому  заменим  его  через  l_т (¶t/¶y) .  Тогда  уравнения  примут  следующий  вид:

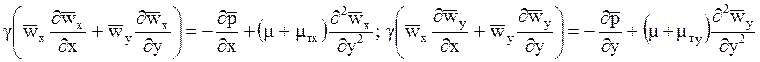
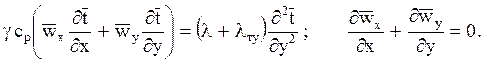
В  этих  уравнениях   m _т    и   l _т -  это  не  характеристики  физических  свойств  среды, так  как  они  зависят  от  турбулентности  потока  и  меняются  по  его  объёму.  Так,  непосредственно  у  поверхности  тела  поперечные  пульсации,  очевидно,  будут  равны  нулю,  поэтому  нулю  будут  равны  и m _т  с  l _т.  А  вдали  от  поверхности  они  могут  во  много  раз превышать l  и  m.

2.8.  Уравнения  переноса  в  пограничных  слоях

При  движении  сред  с  большими  числами  Рейнольдса  в  пограничном  слое  влияние  сил  вязкости  пренебрежимо  мало.  При  наличии  теплообмена  в  потоке  возникает,  кроме  динамического,  ещё  и   тепловой  пограничный  слой,  который  в  основном  и  определяет  интенсивность  переноса   энергии. 

В  пределах  пограничных  слоёв  скорость,  температура  и  концентрация  асимптотически  приближаются  к   своим   значениям  в  ядре  потока.   За  толщину  слоя  условно  принимают  то  расстояние  по  нормали  от  поверхности,  на  котором  численные  значения  вышеуказанных  величин  отличаются  от    их  значений   в  ядре  потока  на  1%.

Толщины  пограничных  слоёв  настолько  малы  по  сравнению  с  характерным,  определяющим  геометрическим  параметром  обтекаемого  тела,  что  в  большинстве  технических  конструкций  эти  слои  можно  считать  плоскими  и  бесконечно  большими  по  ширине,  то  есть  поля  скоростей,  температур,  концентраций  можно  считать  двухмерными.  Из-за  малой  толщины  слоёв  градиенты  этих  величин  по  нормали  к  поверхности  существенно  больше  градиентов  продольных;  нормальная    к  поверхности  составляющая  скорости  близка  к  нулю,  если  не  применяются  специальные  меры  вроде  вдува  или  отсоса.  Поэтому  и  градиент  давления  в  этом  направлении   можно  принимать  равным  нулю.

При  ламинарном  стационарном  движении    и  постоянных  теплофизических  свойствах   уравнения пограничных  слоёв  выглядят  следующим  образом:

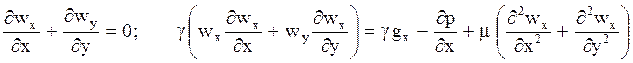
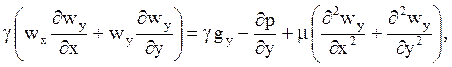
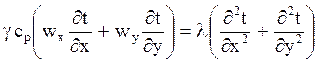
Л.  Прандтль  предложил  упростить  эти  уравнения,  отбросив  члены  малого  порядка,  оценить  который  можно  путём  сравнения  входящих  в  них  величин.  Так,  например,  w_x >> w_y,  характерный  размер  тела  х  намного  больше  толщины  пограничного  слоя  d.  Если  порядок  w_x  и  х  принять  равным   единице,  то  порядок  П(¶w_x/¶x)   тоже  будет  равен  единице . Нуль в уравнении неразрывности может быть только в  том  случае,  когда  оба  члена  имеют  одинаковый  порядок,  поэтому  П(¶w_y/¶y) =1,  стало   быть  П(w_y) = d.  А  так  как  ¶w_x/¶x  и  ¶w_y/¶y  одного  порядка,  то  оба  они  должны  остаться  в  уравнении.