Организация эксплуатации локомотивов в депо Саратов, Технологический процесс ремонта турбокомпрессора ТК-38, страница 13

В результате обработке статистического материала о заходах локомотивов на ПТОЛ, определен параметр закона экспоненциального распределения случайной величины интервала времени между локомотивами. Этот параметр λ= 38.

Состояние системы будем нумеровать по числу заявок, связанных с ней, а именно:

S₀ – система свободна;

S₁ – один канал занят, остальные свободны, очереди нет;

S₂ – два канала заняты, остальные свободны, очереди нет;

S₃ – три канала заняты, остальные свободны, очереди нет;

S₄ – четыре канала заняты, остальные свободны, очереди нет;

S₅ – пять каналов заняты, остальные свободны, очереди нет;

S₆ – все шесть каналов заняты, очереди нет;

S₇ – все шесть каналов заняты, одна заявка стоит в очереди;

S₈ – все шесть каналов заняты, две заявки стоят в очереди;

S₉ – все шесть каналов заняты, три заявки стоят в очереди;

S₁₀ – все шесть каналов заняты, четыре заявки стоят в очереди;

S₁₁ – все шесть каналов заняты, пять заявок стоят в очереди;

S₁₂ – все шесть каналов заняты, шесть заявок стоят в очереди;

Граф состояний представлен на листе 4.

Пусть в начальный момент времени (t=0) система находится в состоянии S₀, хотя это и не имеет значения, так как предельный режим не зависит от начального состояния. Разыграем на оси времени случайный поток заявок, т.е. моментов прихода заявок t₁, t₂, t₃. Для этого с помощью программы Excel и функции случайного числа получаем равномерно распределенные случайные числа в интервале 0…1 (табл. 1.6.)

Таблица 1.6.

Случайные числа

№	Серия локомотива	Случайные числа, xi	Случайные числа, имеющие показательное распределение, Тi	ti=xi+ti-1
	1	2	3	4   0
1	ЭП1	0,794546446	0,14607339	0,15
2	ТЭП70	0,001238751	4,119170228	4,27
3	ТЭП70	0,377101107	0,600148886	4,87
4	ЭП1	0,721295732	0,201049881	5,07
5	ЧМЭ3	0,056708907	1,766045534	6,83
6	ЭП1	0,149501822	1,169505662	8,00
7	ЭП1	0,468718266	0,466309787	8,47
8	ТЭП70	0,493412973	0,434713097	8,90
9	ТЭП70	0,020131407	2,403368698	11,31
10	ЭП1	0,921877428	0,050057234	11,36
11	ЭП1	0,969549312	0,019030118	11,38
12	ЭП1	0,455118958	0,484428583	11,86
13	ТЭП70	0,934617069	0,041611314	11,90
14	ЭП1	0,785566194	0,148523418	12,05
15	ЭП1	0,956918607	0,027099656	12,08
16	ЭП1	0,708969645	0,211656965	12,29
17	ТЭП70	0,452206577	0,488379185	12,78
18	ЭП1	0,582119548	0,332971965	13,11
19	ТЭП70	0,207411175	0,968032064	14,08
20	ТЭП70	0,896476026	0,067251525	14,15
21	ЧМЭ3	0,802376207	0,135493966	14,28
22	ЧМЭ3	0,748053822	0,178634061	14,46
23	ЭП1	0,747914698	0,178748521	14,64
24	ЭП1	0,781580675	0,151653479	14,79
25	ЭП1	0,515138804	0,408196242	15,20
26	ЧМЭ3	0,389518529	0,580211596	15,78
27	ЭП1	0,672801511	0,243879954	16,02
28	ЧМЭ3	0,794966384	0,141203354	16,16
29	ЧМЭ3	0,17618092	1,068457757	17,23
30	ЧМЭ3	0,084146472	1,523197711	18,76
31	ЧМЭ3	0,413831483	0,542951652	19,30
32	ЭП1	0,450317148	0,490955797	19,79
33	ЧМЭ3	0,176040166	1,068949598	20,86
34	ЧМЭ3	0,601792529	0,31251848	21,17
35	ЭП1	0,515750448	0,407466005	21,58
36	ЭП1	0,396475744	0,569317178	22,15
37	ТЭП70	0,799612643	0,137617147	22,28
38	ТЭП70	0,090709732	1,476978851	23,76

Случайные числа, равномерно распределенные в интервале 0…1, вырабатываемые указанным выше или любым другим способом, служат исходным материалом для формирования возможных значений случайных величин с другим законом распределения. При моделировании процессов, протекающих в транспортных системах, могут найти применение непрерывные вероятностные законы распределения.

Для последовательных случайных величин x_i используем указанный закон распределения. Чтобы получить последовательность случайных величин x_i, имеющих показательное распределение:

 (1.28.)

где
частота поступления заявок в систему обслуживания .

Для этого, интегрируя выражение (1.26.) в пределах 0…x_i и приравнивая его к x_I, получим уравнение:

       (1.29.)

Решая это уравнение относительно x_i, имеем

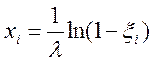  (1.30.)

Учитывая, что случайное число (1-x_i ) подчиняется также равномерному закону распределения в интервале (0…1), выражение (1.25.) можно заменить уравнением:

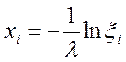      (1.31.)