Курсовое проектирование по "Теории механизмов и машин", страница 61

1. Отрезки, изображающие перемещение , откладывают на новой диаграмме (рис. 11.2, г) либо их переносят с диаграммы S = S() (рис. 11.2, в).

2. Для каждого положения точки B (для каждого значения S) находят длину вектора v_qB и откладывают его перпендикулярно перемещению S. Условно для положительного направления вектора v_qB принята фаза удаления при вращении кулачка по часовой стрелке. Соответственно в фазе сближения вектор v_qB — отрицательный. Аналоги скоростей, изображаемые на разных диаграммах, имеют разные масштабы. Для их согласования отрезки  в мм, взятые из диаграммы v_qB = v_qB(φ), умножают на отношение масштабов. Таким образом, отрезок, изображающий вектор v_qB на диаграмме v_qB = v_qB(S), равен:

                                        .                           (11.12)

Из концов векторов v_qB должны проводиться лучи под углами передачи m, которые в соответствии с правилом центра вращения кулачка проходят через центр его вращения. В начале проектирования эти углы неизвестны, но их минимальные значения определяют через допускаемые углы давления

                                       .                           (11.13)

3) Для нахождения положения центра вращения кулачка концы векторов v_qB объединяют плавной кривой, образующей диаграмму v_qB = v_qB (S). Касательно к диаграмме проводят лучи под углами  и  к оси ординат (рис. 11.2, г). Точка пересечения граничных лучей является оптимальной для положения центра вращения кулачка из условия минимальных его размеров. Возможные положения центра вращения, для которых выполняется условие  < , могут находиться между продолжениями граничных лучей ниже точки их пересечения, но размеры механизма не будут минимальными.

4) Величину смещения e определяют кратчайшим расстоянием  (рис. 11.2, г) от центра вращения до траектории движения толкателя. Действительное смещение eопределяют делением отрезка  на масштаб m_S с последующим округлением до стандартного целого числа в мм.

5) Начальный радиус r_o определяют отрезком от центра вращения кулачка до нижней точки перемещения толкателя

                                       .                          (11.14)

Начальный радиус следует округлить до стандартного значения из ряда Ra 40 по ГОСТ 6636–69: до 22 мм каждое целое значение; далее 24, 25, 26, 28, 30, 32, 34, 35, 36, 38, 40, 42, 45, 48, 50 мм.

Б. Кулачково-коромысловый механизм.

Правило центра вращения кулачка справедливо и для механизма с коромыслом. В произвольно выбранном масштабе m_l строят коромысло l в крайних положениях с заданным размахом y_max (рис. 11.3).

В кулачково-коромысловом механизме задан закон движения коромысла в виде аналога углового ускорения — второй производной углового перемещения по обобщенной координате. Графическим интегрированием получают диаграммы аналога угловой скорости и угла поворота коромысла. Образец листа 4 курсового проекта для иллюстрации проектирования кулачково-коромыслового механизма приведен на рис. 11.4.

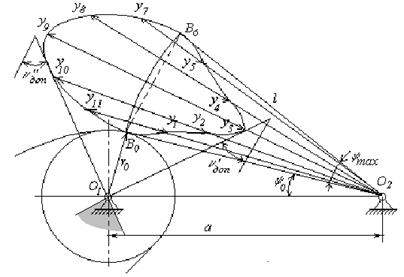
Рис. 11.3

Масштаб углового перемещения коромысла может быть выражен в мм/град или мм/рад. В первом случае

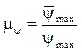                                           ,                               (11.15)

во втором случае

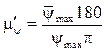                                         ,                            (11.16)

где  — максимальная ордината на диаграмме ψ = ψ(φ), мм; y_mаx — максимальное заданное угловое перемещение, град.

Масштаб первой производной углового перемещения в мм:

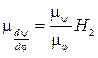                                          .                              (11.17)

Векторv_qB определяют по формуле:

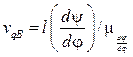                                      .                           (11.18)

Рис. 11.4

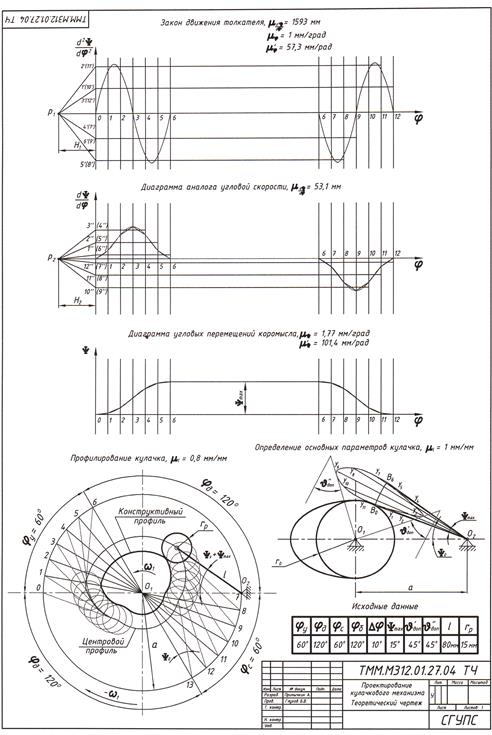
Практически величина v_qB составляет часть от длины коромысла l, например, 0,38. Для построения диаграммы v_qB = v_qB (S) в этом случае дугу В₀–В₆, очерченную радиусом l(рис. 11.3), размечают, откладывая текущие углы поворота коромысла для каждого положения кулачка в градусах, взятые из диаграммы ψ = ψ(φ). При этом величины углов определяют делением ординаты диаграммы ψ = = ψ(φ) на масштаб .