Курсовое проектирование по "Теории механизмов и машин", страница 48

2. В положительных колесах по сравнению с нулевыми колесами увеличиваются диаметры вершин и впадин, в результате они не смогут вписаться в делительное межосевое расстояние a. На картине зацепления в этом случае будет интерференция (наложение) зубьев шестерни и колеса (рис. 8.4, б) и передачу нельзя будет собрать при межосевом расстоянии a_w = a.

3. Для обеспечения правильного зацепления необходимо увеличить межосевое расстояние a_w, чтобы устранить интерференцию. Для этого оси колес в первом приближении следует раздвинуть на сумму смещений x_S = m (x₁+ x₂). Радиальный зазор при этом должен оставаться стандартным (0,25 m). Однако при этом между нерабочими поверхностями зубьев возникнет недопустимо большой боковой зазор, который регламентируется стандартами. В таком зацеплении (рис. 8.4, в) при изменении направления вращения колес (реверсе) возникает «мертвый ход» и дополнительные динамические нагрузки.

4. Проблему решают, уменьшая суммарное смещение x_S на величину так называемого уравнительного смещения Dym, где Dy — коэффициент уравнительного смещения. При этом образуется зацепление с нормированным боковым зазором j_n, но для обеспечения стандартного радиального зазора зубья колес необходимо «обрезать» на величину Dym (рис. 8.4, г). Из приведенных рассуждений следует, что коэффициент воспринимаемого смещения равен:

y = x₁ + x₂ – Dy = – Dy.                       (8.21)

Высота зуба при этом уменьшается на величину уравнительного смещения:

h = m (2,25 – Dy).                            (8.22)

Межосевое расстояние, выраженное через углы профилей:

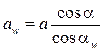                                         ,                              (8.23)

где α_w — угол зацепления, это угол профиля по начальным окружностям, определяемый как угол между линией зацепления, проведенной касательно основным окружностям, и перпендикуляром к межосевой линии. Из формулы (8.23) можно определить угол зацепления при известных прочих параметрах:

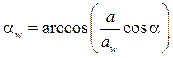                                  .                        (8.24)

При известных смещениях угол зацепления определяют по формуле:

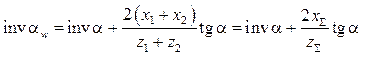               .     (8.25)

Начальные диаметры при известном межосевом расстоянии могут быть рассчитаны по формулам:

d_w1 = 2a_w/(i₁₂ + 1).  d_w2 = i₁₂d_w1.                  (8.26)

Они также могут быть определены по формуле:

                                         .                                      

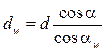Диаметры вершин с учетом (8.11) рассчитывают по формуле:

d_a = m (z + 2 + 2x – 2Dy).                      (8.27)

Диаметры впадин:

d_f = m (z – 2,5 + 2x).                          (8.28)

В формулах (8.27) и (8.28) учтено увеличение диаметров колес на удвоенную величину смещения, а в формуле (8.27) — кроме увеличения еще и уменьшение диаметра вершин на удвоенное уравнительное смещение, выполняемое для устранения бокового зазора по нерабочим профилям зубьев. Радиальный зазор с всегда остается равным стандартной величине 0,25m.

Коэффициент перекрытия определяет среднее число зубьев, одновременно находящихся в зацеплении. При его увеличении повышается плавность работы передачи. Реально в прямозубом зацеплении одновременно работают либо одна пара зубьев, либо две пары. Но чем выше коэффициент перекрытия, тем прочнее передача, так как зубья работают менее напряженно. Его расчет ведут по формуле:

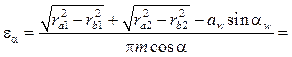
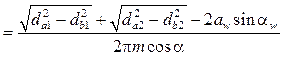                       .             (8.29)

Для определения коэффициента перекрытия используют также другую формулу (из ГОСТ 16532–70):

                            (8.30)

Толщина зуба по окружности произвольного диаметра d_y:

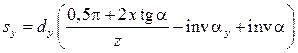                      .           (8.31)

В частности, для проверки отсутствия заострения по вершинам зубьев шестерни рассчитывают s_a по формуле (8.31), в которой вместо d_y и a_y ставят d_a и a_a. Угол a_a рассчитывают по формуле (8.22). В результате для окружности вершин имеем:

                                     ;                                  

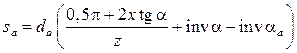                      .           (8.32)