Курсовое проектирование по "Теории механизмов и машин", страница 35

                              ; .                     (5.8)

Для определения полной реакции  на плане сил выполняют векторное сложение по уравнению

                                                                          (5.9)

путем соединения точек 7 и 1. Модуль полной реакции

                                         .                                       

В) Векторное уравнение для звена. Для определения реакции в средней кинематической паре С диады составляют векторное уравнение сил, действующих на одно звено диады, например, на звено 3:

                               .                             

3–4    4–5     5–6    6–7     7–3

Искомый вектор  определяют замыканием части векторного многоугольника, построенного по уравнению (5.6), путем соединения точек 7 и 3 со стрелкой, направленной в точку 3. Аналогичный отрезок со стрелкой противоположного направления получится при составлении векторного уравнения для звена 2. В итоге получится . Оба вектора равны по модулю, направлены в противоположные стороны и приложены к разным звеньям. По этим причинам они не были включены в уравнение (5.6). Модуль реакции определяют по формуле (5.8).

5.3. Силовой расчет диады 4–5

Реакции в кинематических парах диады 4–5 такого же вида (второго), как диада 2–3, определяют аналогично. В соответствии с циклограммой (табл. 2.1), когда в цилиндре С происходит всасывание с силой сопротивления F_с, направленной против движения, в цилиндре Е, к поршню которого приложена движущая сила F_д в направлении движения, происходит такт «расширение» Если студенту задается такт «расширение» в цилиндре С, то на поршень Е будет действовать сила сопротивления F_с, а на поршень С — движущая сила F_д. Расчетной схемой является план положений диады, к которому приложены действующие силы F_д, G₄, F_и4 и момент M_и4, определяемые по формулам (5.1)…(5.4). Искомыми будут реакции , ,  и R₄₅. Порядок силового расчета диады аналогичен изложенному в п/п. 5.5.2:

1)  Моментное уравнение относительно точки Е для определения составляющей реакции :

                        ,                 (5.10)

где ED, h₁ и h₂ — плечи сил на плане диады (рис. 5.3).

2)  Векторное уравнение для диады:

                 ,       (5.11)

решая которое, определяют R₀₅,  и .

3) Векторное уравнение для звена 4:

                                ,                     (5.12)

Рис. 5.3

из которого находят . Модули реакций определяют по формуле (5.8). План сил диады 4–5 приведен на рис 5.4.

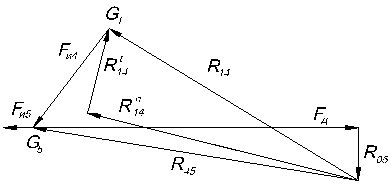
Рис. 5.4

5.4. Силовой расчет начального звена

Действующие силы через реакции в парах передаются на начальное звено. Эквивалентом этих сил по модулю является уравновешивающий момент . Его определяют из уравнения моментов относительно центра вращения кривошипа А:

                        ; ,              (5.13)

где h₁ и h₂ — плечи сил на плане начального механизма (рис. 5.5).

Рис. 5.5

В точках В и D звена 1 прикладывают реакции  и . Реакцию  во вращательной паре определяют из векторного уравнения:

                                  .                        (5.14)

Пример плана сил начального звена приведен на рис 5.6.

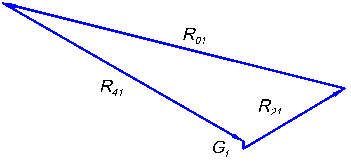
Рис. 5.6

5.5. Расчет мощностей

Для каждого положения начального звена мгновенная мощность для механизмов двигателей

                                         ,                              (5.15)

где P_д — мощность движущих сил, Вт.

                                           ;                                 (5.16)

 — мощность сил трения, Вт; ее определяют как сумму мощностей трения во всех кинематических парах

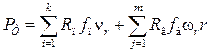                              ,                    (5.17)

где k — число поступательных пар; в механизме ДВС k= 2; m — число вращательных пар; m= 5;  — реакция в поступательной паре, Н (R₀₃, );  — реакция во вращательной паре (R₀₁, R₁₂, R₁₄, R₂₃, R₄₅);  — коэффициент трения в поступательной паре; рекомендуется принимать  = 0,1;  — коэффициент трения во вращательной паре  = 0,08;  — относительная скорость в поступательной паре, м/с (, );  — относительная угловая скорость, с^-1; определяется с учетом знаков угловых скоростей  и  соседних звеньев по формуле