Высота до
постоянной хорды 
определяется как кратчайшее
расстояние от вершины зуба до средней точки постоянной хорды:
= 0,5(da – d – 
tga). (8.53)
Контрольные параметры рассчитывают по программе ТМ21.
В распечатке на рис. 8.16 приведен пример контрольных параметров. Из примера следует, что показать длину общей нормали следует на зубьях шестерни (zw1 = 2), так как студенту разрешено показывать 3 зуба, а число зубьев обхвата зубьев колеса zw2 = = 4. Для построения проводят касательную к основной окружности шестерни с точкой касания примерно на середине впадины и в точках касания ее с эвольвентами ей перпендикулярно — выносные линии размера W.
Рис. 8.16
Постоянную хорду 
и высоту зуба до постоянной хорды 
показывают на одном зубе любого колеса..
1. Каково основное условие синтеза зубчатого зацепления?
2. Какие профили колес называются сопряженными?
3. Сформулируйте основную теорему зацепления и ее следствие.
4. Какие кривые удовлетворяют основной теореме зацепления с учетом дополнительных требований?
5. Как строится эвольвента окружности графически и по данным, полученным аналитически?
6. Какая окружность называется основной?
7. Что называется углом профиля эвольвенты? Укажите на картине зацепления угол профиля по окружности вершин.
8. Перечислите свойства эвольвенты
9. Что такое шаг зубчатого колеса?
10. Что такое модуль колеса?
11. Какая окружность называется делительной?
12. Каковы основные параметры исходного контура?
13. Какие передачи различают в зависимости от знака смещения?
14. В чем причина изменения качественных характеристик колес, нарезанных со смещением инструмента?
15. При каких смещениях повышается изгибная и контактная прочность зубьев?
16. Какие параметры изменяются в положительной передаче?
17. При каких числах зубьев ножка зуба будет подрезана?
18. Что необходимо сделать для устранения подрезания?
19. При каких условиях будет заострение зуба?
20. Что такое линия зацепления, активная линия зацепления?
21. Как определяется угол зацепления? Какова его роль?
22. Как точка контакта сопряженных профилей перемещается по активной линии зацепления и по профилям?
23. Что такое коэффициент перекрытия?
24. Как влияет коэффициент перекрытия на прочность зацепления и плавность работы?
25. Какие задачи решаются выбором оптимальных коэффициентов смещения?
26. При каких условиях износостойкость будет оптимальной?
27. Что является признаком повышения контактной прочности?
28. Как влияет смещение на изгибную прочность зубьев?
Проектирование планетарных механизмов состоит из двух этапов: выбор схемы и определение чисел зубьев колес. При назначении чисел зубьев необходимо учитывать ряд ограничений:
а) числа зубьев должны быть целыми числами;
б) выбранные числа зубьев должны давать передаточное отношение i с допустимой точностью Di; по ГОСТ 2185–66 при i ³ 3,5 Di = ±4 %;
в) рекомендуется для большинства случаев использовать нулевые прямозубые колеса с ограничениями для колес с наружными зубьями по минимально допустимым числам зубьев из условия неподрезания — zн. min = 17, для колес с внутренними зубьями из условия отсутствия интерференции — zв. min = 19 (см. табл. 9.1). Другие ограничения рассмотрены ниже.
Условия синтеза рассмотрены на примере простого планетарного механизма (редуктор Джеймса, рис. 9.1). Механизм имеет два зацепления: внешнее z1/z2 и внутреннее z2/z3.
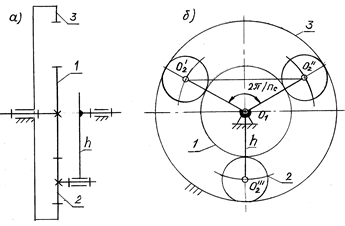
Рис. 9.1
1. Условие соосности предполагает равенство межосевых расстояний обоих зацеплений, так как оси центральных колес 1 и 3 совпадают, а сателлит 2 входит в оба зацепления:
а12 = а32 или r1 + r2 = r3 – r2.
Так как r = mz/2, можно записать:
z1 + z2 = z3 – z2, (9.1)
откуда
z2 = (z3 – z1)/2. (9.2)
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.