Курсовое проектирование по "Теории механизмов и машин", страница 25

Следует помнить важное правило: для нанесения отрезка на план физическую величину умножают на масштаб. Построения начинают с нанесения на план элементов стойки: неподвижных шарниров и направляющих. Прежде всего это центр вращения кривошипа 1 — точка А (рис. 4.1).

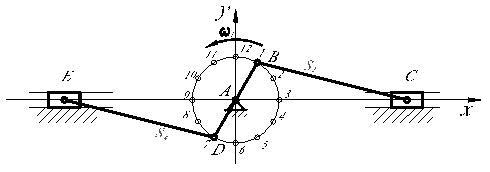
Рис. 4.1

Радиусом АВ описывают окружность — траекторию точки В, которую делят на 12 равных частей и ставят в них шарниры, обозначая цифрами в соответствии с часовым циферблатом. Через точку А проводят горизонтальную прямую — траекторию движения ползунов.

Положения подвижных шарниров находят методом засечек. Для этого раствором циркуля ВС с ножкой в точке В проводят ряд окружностей до пересечения с другими окружностями или направляющими. В пересечении ставят шарниры.

Траекторию центра тяжести шатуна получают соединением плавной кривой точек S₂, нанесенных на положения шатунов путем откладывания отрезков ВS₂. Фрагмент листа 1 с планом заданного положения приведен на рис. 4.2.

4.2. План скоростей

План скоростей — это векторный многоугольник, изображающий величины и направления скоростей точек механизма в заданном положении начального звена. При использовании компьютерных расчетов студент строит один план скоростей и один план ускорений. При отсутствии таких расчетов студент строит по 6 или 12 планов (по указанию руководителя проекта).

Начальное звено — это звено, которому задается обобщенная координата. Для кривошипа, совершающего полный оборот, это угол поворота , отсчитываемый от положительного направления оси x в направлении против часовой стрелки. Начальному звену также задается кинематический параметр — угловая скорость w₁. Так как она задана постоянной, угловое ускорение кривошипа e₁ равно нулю. Для технологических машин начальное звено — ведущее, для двигателей — ведомое, но для определения кинематических и силовых параметров это не принципиально. Основная цель назначения начального звена — упрощение расчетов.

По Ассуру плоский рычажный механизм может быть образован из начального механизма I класса и присоединенных структурных групп. Так как кинематика начального звена известна (, w₁, e₁), то кинематический анализ диадного механизма сводится к исследованию кинематики групп Ассура.

Анализ плана положений механизма ДВС (рис. 4.2) показывает, что в диаде 2–3 неизвестна кинематика средней вращательной кинематической пары C, принадлежащей одновременно звеньям 2 и 3. Таким образом, векторные уравнения теоремы о сложении скоростей составляют для внутренней кинематической пары группы Ассура. Система векторных уравнений в движении точки С относительно подвижной точкиВ, условно принятой за неподвижную, и неподвижной направляющей х–х:

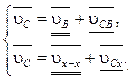                                      ,                             (4.4)

где v_B — абсолютная скорость точки В, м/с; v_CB — относительная скорость вращательного движения; v_x-x — скорость направляющей; в кривошипно-нолзунном механизме v_x-x = 0; v_Cx — относительная скорость поступательного движения.

Векторы скорости рычажного звена направлены перпендикулярно звену в сторону вращения. Модуль линейной скорости, м/с:

                                            .                                   (4.5)

Для ее изображения на плане выбирают масштаб плана скоростей , мм/(м×с^-1):

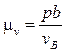                                             ,                                    (4.6)

где pb — отрезок на плане скоростей, изображающий скорость точки В, мм.

Длину отрезка pbпринимают такой, чтобы получился масштаб, удобный для расчетов. Так, например, при скорости v_B = 4,8 м/с можно принять длину pb = 96 мм. При этом масштаб  = 96/4,8 = = 20 мм/(м×с^-1). Следует помнить, что на чертежах отрезки, изображающие различные физические величины (скорость v, м/с; ускорение a, м/с²; силу F, Н; время t, с и т.д.), откладывают в миллиметрах.

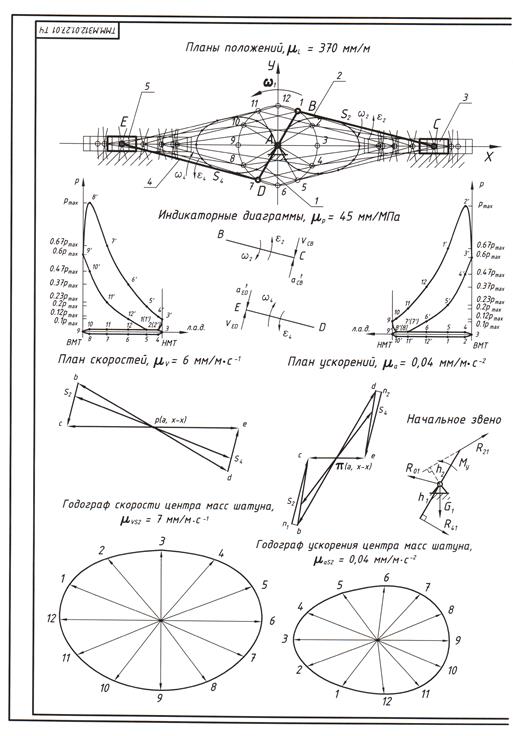
Рис. 4.2

В системе векторных уравнений (4.4) v_C — искомая скорость, неизвестная по величине и направлению, скорости v_B и v_x-x — известные (подчеркнуты двумя чертами), а относительные скорости v_CB и v_Cx — известны только по направлению (подчеркнуты одной чертой). Пересечение их направлений дает графическое решение задачи определения искомой скорости v_C. На свободном поле чертежа выбирают положение полюса плана скоростей p(рис. 4.3).