Курсовое проектирование по "Теории механизмов и машин", страница 32

Б) Компьютерная программа

Кинематические параметры кривошипно-коромыслового механизма могут быть рассчитаны по программе ТМ23 в системе GWBASIC. Схема на рис. 4.6 — типовая. В заданиях на курсовой проект таких нет. Необходимо вводить угол между осями заданной схемы и типовой.

В механизме качающегося конвейера (рис. 2.10, а) следует рассчитать кинематику цепи ABCD, содержащей диаду первого вида. Направление оси типовой схемы — вдоль оси x. Ось заданной схемы — AD, она соединяет оси вращения кривошипа 2 и коромысла 3. Угол между осями xи AD:

                                        .                             (4.55)

В механизме пресса (рис. 2.11, а) угол ψ определяют по формуле:

                                   .                        (4.56)

В механизме подачи заготовок (рис. 2.12, а):

                                  .                       (4.57)

В механизме стана холодной калибровки труб (рис. 2.13, а) угол между осями определяют по формуле (4.55):

                                       .                                     

Угол между осями ψ обычно не совпадает с одним из заданных положений кривошипа. Для того, чтобы вычислить кинематические параметры во всех 12 положениях, вводят начальный угол φ_1.0, отличный от 90°, исходя из следующего примера по исходным данным задания 7–7: x = 0,29 м, у = 0,05 м (рис. 2.10, а). Угол между осями:

                               .                             

Ближайшее в направлении против часовой стрелки положение кривошипа — 2 (). Для расчета кинематики в этом положении необходимо ввести начальный угол:

                                  .                                

Это угол от оси заданной схемы до ближайшего положения кривошипа. Он должен быть . В общем случае

                                         ,                              (4.58)

где n = 0, 1, 2 и т.д. Например, при  . Во всех случаях задают шаг . Пример распечатки компьютерных расчетов по исходным данным задания 7–7 для шести положений кривошипа приведен на рис. 4.12.

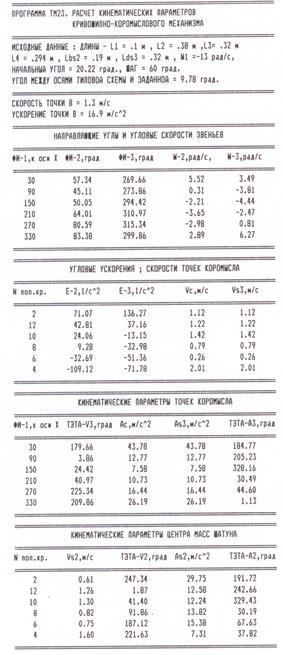
Рис. 4.12

4.5.4. Кривошипно-кулисный механизм

А) Аналитические выражения

Расчетная схема механизма представлена на рис. 4.13. Длины звеньев заменены векторами ,  и .

Особенностью механизма является то, что точка В принадлежит одновременно трем звеньям. Точка кривошипа В₁ и точка В₂ камня кулисы имеют общую ось и одинаковые кинематические параметры. Точка В₃ на кулисе меняет свое положение в зависимости от координаты кривошипа. Ее кинематические параметры переменны. Координата точки В₃:

. (4.59)

Угловая координата кулисы

                         .              (4.60)

Угловая скорость кулисы

                                 .                      (4.61)

Относительная скорость

                                 .                      (4.62)

Кориолисово ускорение

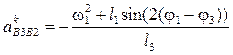                            .                  (4.63)

Относительное ускорение

                     .           (4.64)

Угловое ускорение кулисы:

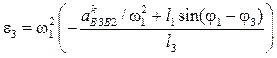                        .             (4.65)

Скорость и ускорение точки В₁ определяют по формулам (4.5) и (4.12). Скорости и ускорения точек В₃, D и S₃ определяют по формулам, аналогичным (4.53) и (4.54):

                         ; ; ;                      

          ; ; .       

Направления векторов линейных скоростей определяют в соответствии с табл. 4.1. Пример распечатки компьютерных данных по исходным данным задания 6–6 приведен на рис. 4.14.

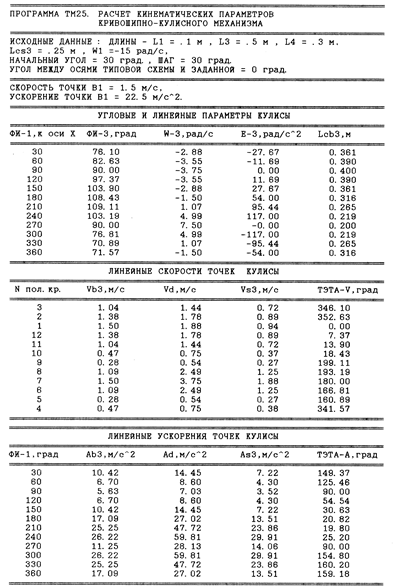
Рис. 4.14

Выводы

1. Кинематические диаграммы — наглядное графическое изображение в декартовых координатах перемещений, скоростей и ускорений точки звена, движущегося прямолинейно, в функции времени, полученных методом планов или рассчитанных аналитически.

2. Годограф — графическое изображение векторов с изменяющимися направлениями в полярных координатах.

3. Графическое дифференцирование позволяет по диаграмме перемещений получить диаграммы скоростей и ускорений.

4. Аналитические выражения для определения кинематических параметров составляют, используя метод замкнутых векторных контуров и координатный метод.