Направления векторов 
берут из плана ускорений или из
распечаток. Момент сил инерции Ми равен:
. (5.3)
Он направлен против вектора углового ускорения. Вес звеньев имеет постоянное направление — вертикально вниз; его модуль в Н:
,
(5.4)
где g — ускорение свободного падения; g = 9,81 м/с2.
Силы движущие Fд, сопротивления Fс, тяжести G, инерции Fи и моменты сил инерции Mи являются заданными, реакции в кинематических парах R и уравновешивающий момент Му — искомые параметры.
Полная
картина силового расчета представлена на листе 1 (рис. 4.2). Он содержит три
расчетные схемы: диады 2–3, диады 4–5 и начального механизма в
масштабе 
в мм/м и три плана сил в масштабе 
в мм/Н. По распечаткам компьютерных данных
необходимо построить два годографа реакций: в декартовых координатах (
) и полярных координатах (одной из реакций:
, 
или 
). Расчетная схема диады 2–3
приведена на рис. 5.1. В диаде 2–3 искомыми являются реакции R12 и R23 во вращательных парах и R03 в поступательной паре.
А) Моментное уравнение. Реакция во вращательной паре неизвестна по
величине и направлению. Для
решения задачи ее раскладывают по двум направлениям: вдоль звена ВС
располагают нормальную составляющую 
, ей перпендикулярно —
тангенциальную составляющую 
. Реакция имеет направление, перпендикулярное
направляющей х–х, ее прикладывают в точке С ползуна.
Для определения составляющей записывают моментное уравнение
относительно точки С:
; 
,
(5.5)
где ВС, h1 и h2 — плечи сил, взятые из чертежа, мм.
В формулу (5.5) масштаб введен для приведения в соответствие
единиц длины. Знаки моментов ставят по общепринятому правилу: «плюс» — против
часовой стрелки, «минус» — по часовой стрелке. Из формулы (5.5) находят в Н:
.
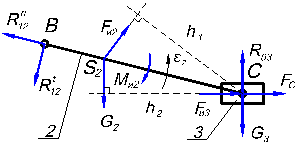
Рис. 5.1
Если получают отрицательное
значение , то его направление будет противоположным
изображенному на схеме (рис. 5.1).
Б) Векторное уравнение для диады. В векторном уравнении записывают векторы всех сил, действующих на диаду, по следующим правилам:
- вначале записывают векторы, известные по величине и направлению; два вектора, известных только по направлению, ставят в конец уравнения;
- последовательно записывают векторы сил, вначале действующих на одно звено, затем на другое;
- нормальные и тангенциальные составляющие располагают рядом; учитывая то, что векторный многоугольник должен быть замкнутым, возможна запись известной составляющей — в начале уравнения, а неизвестной — в конце уравнения.
Векторное уравнение с двумя неизвестными для диады 2–3 имеет вид:
. (5.6)
0–1 1–2 2–3 3–4 4–5 5–6 6–7 7–0
F, Н = 4840 25 6465 17 1930 126
, мм = 73 0 97 0 29
1,9
В формуле (5.6) векторы 
и 
— неизвестные
по модулю, но известные по направлению. В первой дополнительной строке указаны
номера векторов соответствующих сил (начало и конец вектора), во второй — в
качестве примера модули сил в Н, в третьей — длины отрезков, изображающих силы
в мм, в масштабе ,
мм/Н:
.
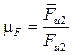(5.7)
|
Рис. 5.2 |
Исходя из приведенных в примере величин
модулей сил и длин отрезков масштаб плана сил 
мм/Н (рассчитывается по
наибольшей силе). Длины отрезков определялись по формуле 
.
Например, 
= 4840·0,015 = 73 мм. Длины отрезков < 2 мм на плане сил не показывают. Вектор показывают в направлении, определенном из
решения уравнения (5.5). Другие векторы вычерчивают в соответствии с уравнением
(5.6): начало вектора прикладывают к концу предыдущего вектора. План
сил диады 2–3 приведен на рис. 5.2.
Так как отрезки
,
и
меньше
2 мм, точки 1 и 2, 3 и 4, 5 и 6 на плане
сил совпадают. Из конца последнего известного вектора 
(фактически
)
проводят направление вектора 
, а из начала первого
вектора, ему перпендикулярно, проводят направление . Точка 7
пересечения векторов определяет длины искомых векторов и
. Модули реакций в Н:
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.
