Курсовое проектирование по "Теории механизмов и машин", страница 52

С учетом того, что при построении диаграмм r₁ = х, а r₂ = g – x, формула расчета g приобретет вид:

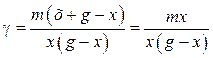                              .                   (8.43)

Диаграмма коэффициента давления g приведена на рис. 8.6, б. Реальные очертания диаграмма имеет в пределах активной линии зацепления А₂А₁, причем в зонах двухпарного зацепления, определяемых размером основного шага p_b, откладываемого от точек А₂ и А₁ в пределах активной линии зацепления, ординаты делят пополам. Из диаграммы видно, что при однопарном зацеплении наименьшие контактные напряжения возникают вблизи полюса зацепления W и соответственно вблизи полюсной линии на поверхности зуба. Влияние смещения на контактную прочность зубчатой передачи может быть оценено по расчетной формуле:

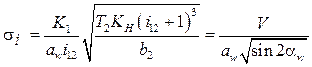                    ,          (8.44)

где K₁ — численный коэффициент; T₂ — вращающий момент на колесе, Н·мм; K_H — коэффициент нагрузки; b₂ — ширина венца колеса, мм; V — параметрический коэффициент, обобщающий все параметры, кроме a_w и .

При увеличении положительного смещения увеличивается угол зацепления. В формуле (8.44) при этом увеличивается знаменатель и снижается рабочее контактное напряжение, что свидетельствует о повышении контактной прочности. В положительном зацеплении межосевое расстояние a_w выше делительного межосевого расстояния a, что создает аналогичный эффект.

Таким образом, при увеличении суммарного смещения контактная прочность повышается, так как увеличиваются угол зацепления и межосевое расстояние.

8.11. Компьютерные расчеты

Геометрию простой зубчатой передачи для построения картины эвольвентного зацепления рассчитывают по программе ТМ21 в системе GWBASIC. Исходные данные вводят в такой последовательности: модуль простой ступени, числа зубьев шестерни и колеса, например: 6, 13, 27. Машина рассчитывает и выводит на печать делительное межосевое расстояние a и минимально допустимый коэффициент смещения x_min из условия неподрезания, который рассчитывается по формуле:

x_min = (17 – z)/17.                             (8.45)

Зубчатую передачу необходимо спроектировать положительной, с коэффициентом суммы смещений  > 0. В этом случае межосевое расстояние a_w необходимо принять больше делительного межосевого расстояния a с условиями:

– a_w должно быть больше a не более чем на модуль зацепления m во избежание заострения зубьев;

– a_w должно быть кратным 5 мм.

Величину a_wстудент назначает самостоятельно и вводит ее в машину, которая после этого рассчитывает коэффициент суммы смещений . При  0,5 следует принимать x₁ = , x₂= 0. При  = 0,5…1,1 разбивку  на x₁ и x₂ студент выполняет с помощью ЭВМ. Цель разбивки коэффициента суммы смещений — оптимизация коэффициентов смещения по двум критериям: изгибной прочности и износостойкости. В обоих случаях в компьютерной программе ТМ21 организуются циклы расчетов геометрических параметров с различными смещениями при сохранении неизменным суммарного коэффициента смещения . В программу заложены коэффициенты смещения шестерни в пределах x₁ = 0,2…1,3 с шагом Δx = 0,1, а коэффициенты смещения колеса рассчитываются по формуле:

x₂ =  – x₁.                                 (8.46)

По результатам расчетов компьютер выдает две таблицы. Первая из них под названием «Оптимизация по изгибной прочности» содержит x₁ и x₂, толщины зубьев шестерни и колеса по окружностям вершин s_a1 и s_a2 и коэффициент перекрытия e_a. Пример распечатки оптимизации смещений по изгибной прочности приведен на рис. 8.7.

Анализ таблицы заключается в том, что студент должен выбрать максимально допустимый коэффициент смещения шестерни x_1max, обеспечивающий наибольшее повышение изгибной прочности при непременном выполнении двух условий: незаострения, выполняемого при s_a1  0,25m и непрерывности зацепления при e_a  1,2. Для этого по табличным данным необходимо построить график s_a1 = s_a1(x₁) и провести на нем линию заострения s_a1доп = 0,25m.

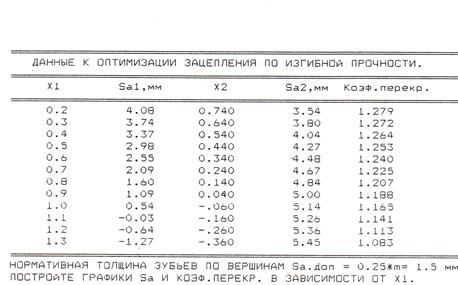
Рис. 8.7

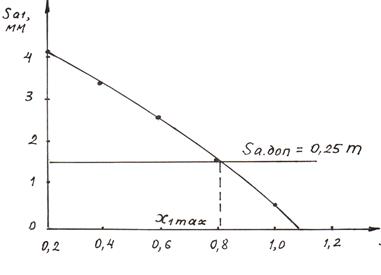
Рис. 8.8