Курсовое проектирование по "Теории механизмов и машин", страница 27

где a_B — линейное постоянное ускорение точки B, м/с ²;  — относительное нормальное ускорение;  — относительное тангенциальное ускорение;  — кориолисово ускорение;  — относительное ускорение.

Линейное ускорение во вращательном движении раскладывают на нормальную и тангенциальную составляющие. Ускорение a_B имеет только нормальную составляющую, так как угловое ускорение  = 0:

                                        .                              (4.12)

Нормальное ускорение направлено к центру вращения. Его определяют также по формуле:

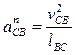                                            .                                 (4.13)

Тангенциальное ускорение  является искомым, но имеет известное направление — перпендикулярно нормальному. Также известно направление относительного ускорения в поступательном движении  — вдоль направляющей. Кориолисово ускорение имеет место только в поступательной кинематической паре и только при вращающейся направляющей (задание 6). Модуль кориолисова ускорения

                                           ,                                (4.14)

где  — угловая скорость направляющей;  — относительная скорость в поступательной паре.

Направление кориолисова ускорения определяют поворотом вектора относительной скорости на 90° в сторону вращения направляющей (). Масштаб плана ускорений в мм/(м×с^-2):

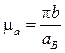                                             ,                                  (4.14)

где  — отрезок, изображающий ускорение точки В.

Например, при a_B = 840 м/с² можно принять  = 84 мм, тогда масштаб  = 84/840 = 0,1 мм/(м×с^-2). Из полюса p(a, x-x) плана ускорений (рис. 4.5) проводят вектор нормального ускорения a_B длиной  к центру вращения кривошипа, от точки В к точке А (рис. 4.2). Из точки bв соответствии с первым уравнением системы (4.11) проводят направление от точки С к точке В вектор нормального ускорения  длиной , а из точки n — направление тангенциального ускорения  перпендикулярно нормальному (перпендикулярно звену ВС).

Решая второе уравнение системы (4.11), при неподвижной направляющей (а_x-x = 0) и отсутствии кориолисова ускорения ( = 0) из полюса p проводят направление  параллельно направляющей до пересечения с вектором  точке c. Направляя искомые векторы в искомую точку c, определяют их направления.

Проводя суммарный вектор bс, на его длине находят точку s₂ по пропорции (4.8) и соединяют ее с полюсом p. Модули искомых ускорений:

                     ; ; .           (4.16)

Модуль углового ускорения шатуна в с^-2:

                                          .                               (4.17)

Направление углового ускорения определяют переносом вектора  в точку С шатуна. На рис. 4.4 его направление положительное (против часовой стрелки).

Для диады 4–5 механизма ДВС записывают систему уравнений, аналогичную (4.11), с индексами при ускорениях, соответствующих системе (4.10):

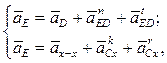                                                            (4.18)

где a_D — ускорение точки D.

                                       .                                    

Из полюса p плана ускорений проводят вектор pd= pb в направлении от точки D к точке A, из его конца — направление  и т.д. в соответствии с уравнениями (4.18) и вышеприведенными действиями. Из анализа плана ускорений механизма ДВС следует, что

                               a_E = –a_C; a_S4 = –a_S2; e₄ = e₄.                             

План ускорений механизма ДВС приведен на рис. 4.5. Примеры построения планов ускорений диад 1-го и 3-го видов приведены в пособии [2].

Выводы

1.  Графический метод планов позволяет определить линейные скорости и ускорения любой точки механизма, угловые скорости и ускорения звеньев механизма в заданном положении начального звена.

2. Кинематический анализ начинают с составления систем векторных уравнений для групп Ассура, где неизвестны скорости и ускорения их средних кинематических пар. Кинематическому анализу предшествует структурный анализ.