Курсовое проектирование по "Теории механизмов и машин", страница 46

                         a = 20⁰,                       где — коэффициент высоты головки зуба;  — коэффициент радиального зазора;  — коэффициент радиуса переходной кривой; a — угол профиля; это угол наклона профиля исходного контура к нормали к его средней линии.

Одним из основных параметров зацепления является модуль. Модуль — линейная величина, в  раз меньшая окружного шага зубьев. Через модуль рассчитывают все геометрические параметры зубчатых колес. Диаметры окружностей вершин, впадин, делительные и основные рассчитывают для единичного зубчатого колеса. Для зубчатого зацепления (пары зубчатых колес) также рассчитывают диаметры начальных окружностей. Геометрические параметры зубчатого колеса внешнего зацепления показаны на рис. 8.1.

Делительной называется окружность, для которой модуль имеет стандарную величину. Делительный диаметр равен

                                              d = mz.                                     (8.4)

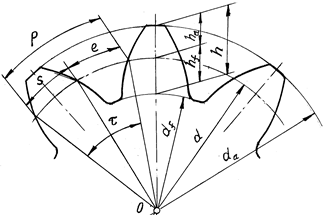
Рис. 8.1

По делительной окружности шаг также будет стандартным. Шаг — это расстояние, измеренное по дуге окружности между двумя одноименными профилями соседних зубьев. Величина шага

                                              p = p m.                                      (8.5)

Эвольвенту описывает каждая точка прямой, перекатывающейся без скольжения по окружности. Основной называется окружность, служащая для образования эвольвенты. Основной диаметр равен

                                d_b = 2r_b = dcosα = mz cosα.                      (8.6)

Высота головки зуба так же, как и некоторые другие параметры колеса, выражается произведением модуля на коэффициент, имеющий в верхнем индексе звездочку. Величина высоты головки:

                                            .                                   (8.7)

Величина радиального зазора:

                                             .                                    (8.8)

Высота ножки зуба больше высоты головки на величину радиального зазора:

                                 .                         (8.9)

Полная высота зуба — это сумма высот головки и ножки:

                          .                (8.10)

Диаметр вершин нулевого колеса определяется суммой делительного диаметра и двух высот головки зуба:

                          .                (8.11)

Диаметр впадин определяется разностью делительного диаметра и двух высот ножки зуба:

                  .       (8.12)

Толщина зуба по делительной окружности обозначается через s. Ширина впадины — e. Для нулевого колеса

s = e = 0,5p = 0,5pm.                         (8.13)

Угловой шаг колеса

                                              t = 2p/z.                                   (8.14)

8.3. Эвольвентные профили зубьев

В общем случае эвольвента (рис. 8.2) описывается двумя уравнениями:

                                      = inva = tga – a;                          (8.15)

                                           r = r_b/cos a,                                 (8.16)

где r — текущий радиус-вектор.

Тригонометрическая функция tga – a называется инволютой (эвольвентной функцией). Таблица инволют приведена в прил. А. Острый угол a между касательной к эвольвенте и текущим радиусом-вектором r, проведенным через точку касания, называется углом профиля (рис. 8.2). Угол, образованный начальным радиусом-вектором эвольвенты и ее текущим радиусом-вектором, называется эвольвентным углом и обозначается .

Угол профиля a_y по любой окружности диаметра d_y определяется по формуле:

                                       a_y = arccos(d_b/d_y).                             (8.17)

Форма эвольвенты зависит только от основного радиуса r_b. Однако профиль зуба может быть очерчен различными участками эвольвенты: крутыми, расположенными вблизи основной окружности, либо более пологими, от нее удаленными. При этом изменяются толщины зубьев и другие параметры, что отражается на прочности и качественных показателях зацепления.

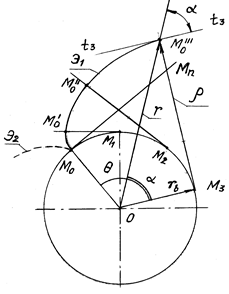
Рис. 8.2

8.4. Геометрия положительного зацепления