Курсовое проектирование по "Теории механизмов и машин", страница 29

Аналитический метод предполагает компьютерные расчеты, которые оформляют следующим образом:

1. Исходные данные, включая расчетную схему.

2. Алгоритм расчета либо блок-схема алгоритма.

3. Распечатка компьютерных данных.

4. Анализ распечаток.

Компьютерные распечатки располагают либо следом за алгоритмом, либо в приложении и оформляют соответственно как рисунки или приложения. Если результаты компьютерных расчетов переписаны с экрана монитора, то такие данные оформляют как таблицы.

4.5.2. Кривошипно-ползунный механизм

А. Аналитические выражения

Расчетная схема кинематической цепи АВС кривошипно-ползунного механизма представлена на рис. 4.8.

Рис. 4.8

По методу замкнутых векторных контуров с осями звеньев 1 и 2 связывают векторы  и . Вектор  — переменной длины. Аналитические выражения выводят из векторного уравнения

                                                                                       путем его проецирования на координатные оси. Углы, определяющие положения векторов (направляющие углы)  и , отсчитывают от оси x в направлении против часовой стрелки при переносе начала вектора в начало координат. В расчеты введены  — относительная длина звена 2 и  — относительная координата центра масс шатуна:

                                  ; .                        (4.21)

Направляющий угол шатуна рассчитывают по формуле:

                                  .                       (4.22)

Угловая скорость шатуна

                             .                  (4.23)

Угловое ускорение

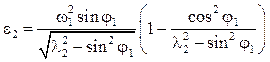                         .               (4.24)

Положительные направления ω₂ и ε₂ соответствуют их направлению против часовой стрелки, отрицательные — по часовой стрелке. Линейная координата точки С ползуна, отсчитываемая от точки А:

                             .                   (4.25)

Расстояние от нижней мертвой точки до ползуна

                                         .                              (4.26)

Дифференцирование выражения (4.25) дает скорость ползуна

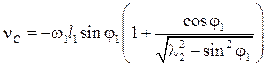                         .              (4.27)

После повторного дифференцирования получают ускорение:

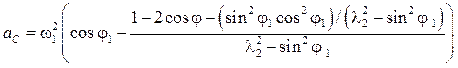      . (4.28)

Положение центра масс шатуна S₂ определяют линейными координатами:

                              ,                    (4.29)

                              .                    (4.30)

При дифференцировании уравнений (4.29) и (4.30) получают выражения для определения проекций скоростей на координатные оси:

                         ,               (4.31)

                         .              (4.32)

Полная скорость

                                      .                           (4.33)

Ее направление определяется с учетом угла  (рис. 4.8):

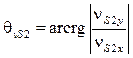                                      .                           (4.34)

Величина угла вектора скорости центра масс шатуна зависит от знака проекций скоростей и определяется из табл. 4.1.

Таблица 4.1

В результате дифференцирования уравнений (4.31) и (4.32) получают ускорения:

             ;  (4.35)

             .  (4.36)

Результирующее ускорение

                                      .                            (4.37)

Его направление определяется углом

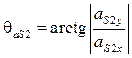                                      .                           (4.38)

Направление вектора  определяют аналогично углу  (см. табл. 4.1). Линейную скорость точки В определяют по формуле (4.5), линейное (нормальное) ускорение точки В — по формуле (4.12). Кинематическая цепь ADEрычажного механизма ДВС (рис. 4.1) с теми же размерами элементов, что и элементов цепи АВС, будет иметь следующие значения соответствующих параметров движения в каждый момент времени:

                  , , , ,                

                      , , , .                    

Направляющий угол шатуна 4