Курсовое проектирование по "Теории механизмов и машин", страница 56

2. Кинематическое условие, выраженное через числа зубьев:

                                          ,                                        откуда

                                                     z₃ = ( – 1) z₁.                                           (9.3)

При точности Di = 0 подбор чисел зубьев ведут в такой последовательности:

а) задаваясь z₁ = 17, 18 и т.д., находят z₃ по формуле (9.3);

б) рассчитывают z₂ из условия соосности — формула (9.2);

в) выполняют проверки по следующим условиям: соседства, сборки и правильности внутреннего зацепления (отсутствие интерференции).

3. Условие соседства предполагает отсутствие интерференции зубьев соседних сателлитов. Для этого необходимо, чтобы расстояние между осями соседних сателлитов  (рис. 9.1, б) было больше диаметра вершин сателлитов d_a2 (двух радиусов 2r_a2). Из D следует:

                        2 (r₁ + r₂) sin (p/n_c) > 2r_a2 = m (z₂ + 2)                      или

                                 (z₁ + z₂) sin (p/n_c) – z₂ > 2,                        (9.4)

где n_c — число сателлитов.

При числе сателлитов n_c £ 3 условие соседства практически всегда выполняется. Недопустимая по условию соседства ситуация показана на рис. 9.2, когда соседние сателлиты невозможно собрать.

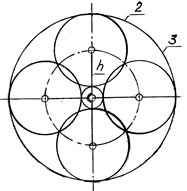
Рис. 9.2

4. Условие сборки предполагает отсутствие интерференции зубьев сателлитов с зубьями центральных колес. Правильная сборка характеризуется тем, что центральные углы между межосевыми линиями соседних сателлитов одинаковы и равны 2p/n_c (см. рис. 9.1, б), т.е. обеспечивается симметрия зон зацепления.

После установки первого сателлита подвижное центральное колесо 1 займет строго определенное положение. При невыполнении условия сборки при установке других сателлитов их зубья не окажутся точно против впадин центральных колес и осуществить сборку колес будет невозможно (рис. 9.3). Условие сборки проверяется по формуле:

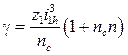                                    = Ц,                           (9.5)

где Ц — целое число; n — любое целое число (1, 2, 3 и т.д.)

Рис. 9.3

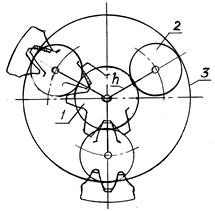
В простейшем случае при n = 0 для механизма любой схемы

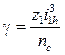                                           = Ц.                                 (9.6)

Для редуктора Джеймса условие сборки (9.6) запишется так:

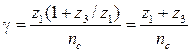                              = Ц.                     (9.7)

5. Условие правильного зацепления предполагает отсутствие интерференции зацепляющейся пары колес внутреннего зацепления. Во внешнем зацеплении с нулевыми колесами при числах зубьев обоих колес больше 17 интерференция в виде заклинивания колес будет отсутствовать. Во внутреннем зацеплении интерференции не будет, если число зубьев колеса с внутренними зубьями z₃ ³ 81, а шестерни с наружными зубьями z₂ ³ 19, как следует из табл. 9.1.

Таблица 9.1

При невыполнении условия правильного зацепления во внутреннем зацеплении будет интерференция (рис. 9.4).

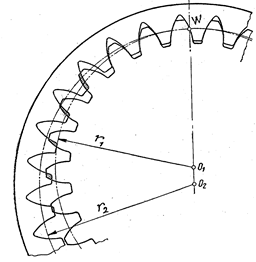
Рис. 9.4

Таким образом, в планетарных механизмах выбор чисел зубьев ограничивается условиями соосности, соседства, сборки и правильности зацепления (интерференцией зубьев во внутреннем зацеплении).

Определение чисел зубьев планетарного механизма по приведенной методике дает повышенные числа зубьев, что при заданном модуле зацепления приводит к большим габаритам передачи. Более рациональным приемом определения чисел зубьев является использование пропорций, учитывающих все ограничения.

Для составления пропорции для редуктора Джеймса числа зубьев z₂ и z₃ и отношение g выражают через число зубьев z₁. Число зубьев корончатого колеса z₃ определяют по формуле (9.3). Число зубьев сателлитов z₂ — из формулы (9.2) с учетом (9.3):

                         .                 (9.8)