Машиностроение \ Теории механизмов и машин

Курсовое проектирование по "Теории механизмов и машин", страница 57

Из условия сборки используют отношение g — формула (9.7). Объединяя все условия, составляют пропорцию:

            .    (9.9)

В соответствии с пропорцией (9.9) числа зубьев колес:

z1 = pnc; z2 = p /2; z3 = p ; g = p(1 – ncn). (9.10)

В выражениях (9.10) р — коэффициент, назначаемый в соответствии с ограничениями, и прежде всего z17. После расчета чисел зубьев выполняют проверки по пяти условиям синтеза.

Пример 9.1. Подобрать числа зубьев z1, z2, z3 и рассчитать КПД редуктора Джеймса (см. рис. 9.1) при  = 6,5; nс = 3; коэффициент полезного действия одного зацепления h = 0,96.

Решение.

Составляем пропорцию (9.10):

                     

                               .                             

Числа зубьев колес и отношение g находим из выражений:

z1 = 3p; z2 = 6,75p; z3 = 16,5; g = 6,5p (1 – 3n).               

В соответствии с численными сомножителями для получения целого числа зубьев необходимо принимать р, кратное 4; принимаем р = 8 из условия получения z1 > 17 (при р = 4 не выполняется условие неподрезания для центрального колеса, так как z1 = = 3·4 = 12 < 17).

z1 = 3×8 = 24; z2 = 6,75×8 = 54; z3 = 16,5×8 = 132; g = 52 (1 – 3n).  

Проверки:

1) условие соосности — формула (9.1):

                               24 + 54 = 132 – 54; 78 = 78;                             

2) кинематическое условие — формула (9.3):

                                    = 1 + 132/24 = 6,5;                                 

3) условие соседства — формула (9.4):

                        (24 + 54) sin(180/3) – 54 = 13,55 > 2;                      

4) условие сборки выполняется, так как g — целое число при любых n (0, 1, 2 и т.д.); либо вторая проверка по формуле (9.7):

                          g =  = 78 — целое число;                        

5) во внутреннем зацеплении интерференция отсутствует, так как z2 > 19, z3 > 81 в соответствии с табл. 9.1 (в зацеплении z2/z3 шестерней является колесо 2, а колесом — колесо 3).

Вывод. Все условия выполнены.

Величину КПД определяем по формуле:

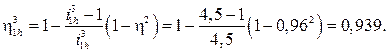                (9.11)

В формуле (9.11) η — КПД одного зацепления.

9.3. Компьютерные расчеты

Оптимальные по габаритам размеры можно получить из компьютерных расчетов. Они позволяют рассчитать числа зубьев планетарного редуктора с любым передаточным отношением путем перебора чисел зубьев в задаваемых пределах от zmin до zmax. Основные принципы синтеза приведены в пп. 9.1 и 9.2.

1. Для редуктора Джеймса записывают условие соосности (9.1) в виде:

z1 + z2 = z3 – z2 = d,                                    откуда числа зубьев

z1 = d – z2;                                 (9.12)

z3 = d + z2.                                  (9.13)

В формулах (9.12) и (9.13) d — аналог делительного межосевого расстояния;

                                а = 0,5m (z1 + z2) = 0,5md.                              

2. Из кинематического условия с учетом равенств (9.12) и (9.13) находят величину d:

                           = 1+ z3/z1 = 1 + (d + z2)/(d – z2),                        

откуда

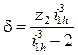                                            .                                  (9.14)

3. Допускаемое отклонение передаточного отношения позволяет определить предельно допускаемые передаточные отношения:

                          ,               (9.15)

где Di — отклонение передаточного отношения.

После подстановки выражений (9.15) в формулу (9.14) получают значения dmin и dmax.

4. Организация циклов. В компьютерных расчетах внутренний цикл образуется изменением величины d, которая задается целыми числами в интервале dmin…dmax. По формулам (9.12) и (9.13) рассчитываются числа зубьев z1 и z3. При этом изменение чисел зубьев сателлитов z2 составляет внешний цикл.

5. Ограничения по числам зубьев осуществляют вводом zmin =  = 17; zmax = 150 (или 200). Вначале принимают z2 = zmin. Компьютер рассчитывает числа зубьев z1 и z3 и проверяет условия z1 ³ zmin и z3 £ zmax. В дальнейшем величина z2 увеличивается на единицу. Пределом является z2 = zmax.

Скачать файл