Курсовое проектирование по "Теории механизмов и машин", страница 42

Приведенный момент инерции определяют из условия равенства кинетической энергии звена приведения сумме кинетических энергий всех звеньев механизма. Для кривошипно-ползунного механизма (см. рис. 4.6) приведенный момент инерции I_п определяют из формулы:

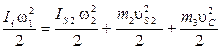                             ,                    (7.11)

Для механизма ДВС вследствие равенства кинематических параметров и масс обеих диад формула (7.11) примет вид:

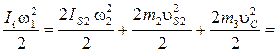
                                 .                       (7.12)

Следует помнить, что полный момент инерции механизма   складывается из момента инерции маховика  и приведенного момента инерции  всех звеньев, кроме начального. Величина  — переменная; величина  — постоянная, она включает в себя собственно момент инерции звена 1 (кривошипа и других связанных с ним элементов, например, зубчатого колеса) и момент инерции маховика, значительно превышающий другие слагаемые. Диаграмму  строят в масштабе , мм/(кг∙м²):

                                       ,                            (7.13)

где  — отрезок, изображающий максимальную величину приведенного момента инерции, мм.

Диаграмму  строят из расчетов по формуле 7.12 либо по компьютерным распечаткам. Диаграмма  с началом координат в точке О (рис. 7.2) одновременно является диаграммой  кинетической энергии всех звеньев, кроме звена приведения. Это следует из выражения:

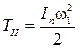                                            ,                                 (7.14)

где 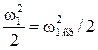 — постоянная величина.

Масштаб диаграммы кинетической энергии всех звеньев, кроме начального в мм/Дж, определяют по формуле:

                                        .                             (7.15)

Если исключить постоянную составляющую диаграммы , т.е. поднять ось абсцисс до точки М, соответствующей минимальной кинетической энергии , то в новой системе координат с началом в точке М появляется диаграмма  в масштабе  (рис. 7.2).

Таким образом, одна и та же кривая изображает диаграмму  в масштабе  и диаграммы  и  в масштабе . Распечатка табл. 11 компьютерной программы ТММ-1, содержащей работу, энергии и моменты инерции, приведена на рис. 7.4.

7.7. Определение момента инерции маховика методом Н.И. Мерцалова

Кинетическая энергия Т всех подвижных звеньев состоит из слагаемых:

                                           ,                                          где  — кинетическая энергия начального звена (в основном маховика), Дж;  — кинетическая энергия всех звеньев, кроме начального.

При динамическом синтезе удобно пользоваться зависимостью приращения кинетических энергий — формула (7.4), из которой находят:

                                       ,                            (7.16)

где  — приращение кинетической энергии начального звена (маховика).

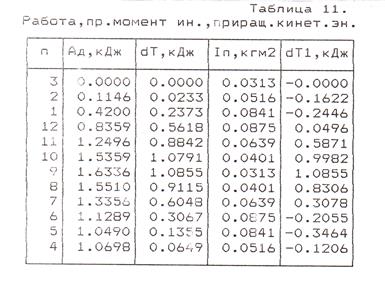
Рис. 7.4

Выражение (7.16) составляет основу метода Мерцалова. Для определения момента инерции маховика необходимо иметь диаграмму приращения кинетической энергии маховика. Данные для ее построения получены в пп. 7.5 (ΔТ) и 7.6 (ΔТ_II).

Известно, что угловая скорость кривошипа w₁ колеблется внутри цикла между значениями w_1min и w_1max. Следовательно, изменяется и кинетическая энергия звена приведения в пределах от  до . Наибольший перепад кинетической энергии маховика

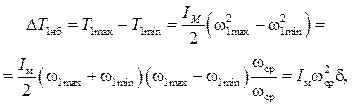
откуда

                                      .                           (7.17)

Для определения отрезка на диаграмме, изображающего величину (см. рис. 7.2), по касательным к диаграмме  = = (j) в точках наибольшего максимума и наименьшего минимума проводят две горизонтальные прямые до пересечения с осью ординат в точках А и Б. Отрезок АБ соответствует наибольшему перепаду кинетической энергии, который должен взять на себя маховик. Величина наибольшего перепада кинетической энергии маховика

                                        .                                      

В окончательном виде формула (7.17) примет вид:

                                     .                          (7.18)