Свойства кристаллических твёрдых тел. Колебания частиц в кристаллической решетке. Уравнение состояния твердого тела. Электронная подсистема твердого тела

НАЦИОНАЛЬНЫЙ ИССЛЕДОВАТЕЛЬСКИЙ УНИВЕРСИТЕТ МЭИ

О.А. Синкевич

ФИЗИКА ТВЕРДОГО ТЕЛА

Часть I

ВВЕДЕНИЕ

Физика твердого тела является одним из важных разделов физики конденсированных систем — науки о физических свойствах систем, состоящих из большого числа сильно взаимодействующих частиц. Даже классическая теория таких систем является чрезвычайно сложной, а в данном случае важную роль играют квантовые процессы. Однако в отличие от плотной плазмы, жидкостей (классических и квантовых), стекол и т. д. можно весьма далеко продвинуться в изучении так называемых кристаллических твердых тел (или просто кристаллов). Последнее связано с наличием у кристаллов определенной симметрии в расположении отдельных частиц (или, как говорят, существованием дальнего порядка). В настоящее время некристаллические твердые тела изучены не столь детально и их глубокое исследование только начинается.

В данном пособии, используя симметрию кристаллов, изучаются простые модели, описывающие колебания кристаллической решетки и структуру энергетического спектра электронов. Обсуждается также статистика электронов и фононов в твердых кристаллических телах, получены основные термодинамические характеристики кристаллов. Основное внимание уделено выявлению физики рассматриваемых явлений и получению количественных оценок.

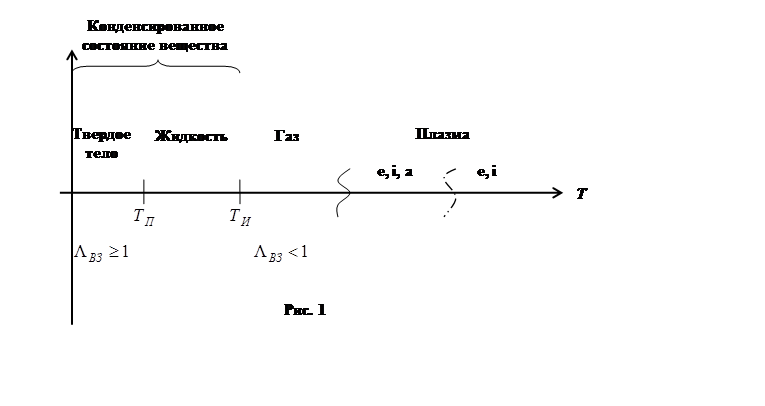
Рассмотрим, как располагаются различные состояния чистого вещества (например, аргона) в зависимости от температуры (рис.1).

При достаточно высоких температурах вещество находится в плазменном состоянии. Причём, при высоких температурах это полностью ионизированная плазма, состоящая из электронов и ионов, а в диапазоне при более низких температур частично ионизированная плазма, содержащая, помимо электронов и ионов, атомы и молекулы.

При понижении температуры плазма переходит в газ. Известно, что нет фиксированной температуры, при которой газ превращается в плазму, но существует область температур, в которой и осуществляется переход от плазмы к электронейтральному газу. Диапазон переходной области, по порядку величины, совпадает с температурой равной потенциалу ионизации рассматриваемого вещества. Если понижать температуру газа, то при достижении температуры кипения (испарения)  газ конденсируется и переходит в жидкость. При дальнейшем понижении температуры осуществляется переход из жидкого состояния в твёрдое при температуре плавления.

Для количественной характеристики состояния чистого вещества используем  безразмерный параметр 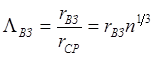, представляющий собой отношение радиуса взаимодействия частиц вещества  при данной температуре к среднему расстоянию между частицами вещества.

Обычно твёрдое и жидкое состояние объединяют в одно, так называемое, конденсированное состояние вещества, где > 1, тогда как в газе  < 1.

Рассмотрим использование безразмерного критерия 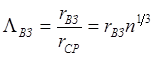 для классификации состояния рассматриваемого вещества.

Любое состояние вещества определяется характером силового взаимодействия частиц, образующих это вещество. Суммарная сила взаимодействие двух частиц складывается из двух

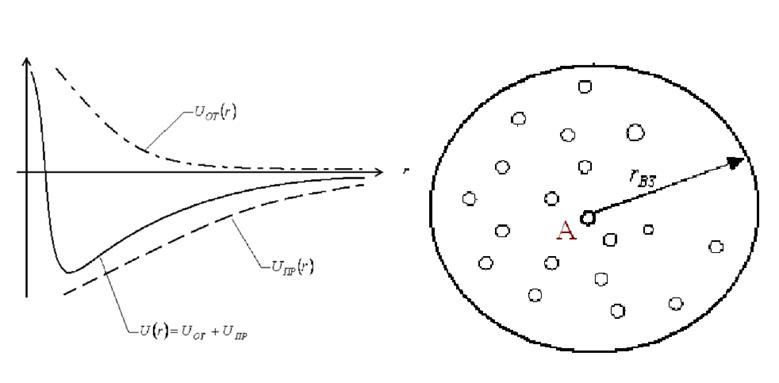
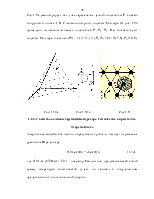
Рис.2                                                                                  Рис.3

составляющих: силы отталкивания  и силы притяжения . На малых, по сравнению с характерными размерами частиц, расстояниях действует квантовый эффект, который приводит к отталкиванию, а при больших – силы взаимодействия вообще ослабевают. На рис.2 представлена характерная картина потенциала взаимодействия, применимая как для газа, так и для жидкости и твёрдого тела.

Рассмотрим частицу А (рис.3), вместе с частицами, с которыми она взаимодействует в сфере радиуса . Определим радиус взаимодействия , как расстояние между частицами, на котором они при данном значении средней энергии ещё могут взаимодействовать. Вычислим число частиц, находящихся в сфере с радиусом , где происходит взаимодействие.

Как оценить радиус взаимодействия? Это можно сделать, зная энергию (температуру), при которой находится вещество, и определяя радиус взаимодействия из условия - энергия взаимодействия равняется известной средней энергии . Зная вид функции  можно найти радиус взаимодействия = . Взаимодействовать с данной частицей А будут только те частицы, которые попадут внутрь сферы с этим радиусом . Очевидно, что число частиц попавших в сферу радиусом  . связано с общим имеющимся количеством частиц. Среднее расстояние между частицами равно .

Отсюда следует, если среднее расстояние между частицами больше радиуса взаимодействия , то частицы практически не будут взаимодействовать. Поэтому можно ввести безразмерный критерий, представляющий собой отношение радиуса взаимодействия к среднему расстоянию между частицами

.

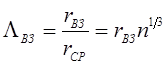Из этой формулы видно: с уменьшением числа частиц, значение критериябудет уменьшаться. Так для разреженных газов  (для идеального газа , но не за счёт того, что концентрация равна нулю, а потому что частицы в нём не взаимодействуют). При больших плотностях частиц (рис.4), когда   возникает совсем другая ситуация, при расчёте которой возникают значительные трудности.