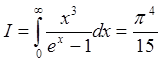Свойства кристаллических твёрдых тел. Колебания частиц в кристаллической решетке. Уравнение состояния твердого тела. Электронная подсистема твердого тела, страница 17

                                              (4.16)

откуда получаем

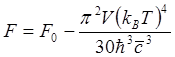                                                         (4.17)

Теперь легко, пользуясь известными термодинамическими соотношениями, получить выражение для внутренней энергии фононов

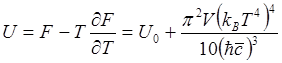                                (4.18)

Физический смысл этого соотношения весьма прост: число фононов с энергией есть ~ Т³, следовательно U ~ Т⁴.

4.2.2.Случай высоких температур

При  << для всех ветвей из (4.4) получаем

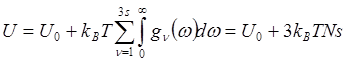                               (4.19)

где использовано условие нормировки (4.6).

Для теплоемкости фононов в случае высоких температур из (4.19) находим

                                  (4.20)

4.2.3. Случай промежуточных температур

В общем случае при вычислении термодинамических функций необходимо знать вклад в как акустических, так и оптических фононов. Для учета вклада оптических фононов обычно используют модель Эйнштейна, суть которой состоит в пренебрежении зависимостью  от . Таким образом, полагают, что  (здесь ~10¹³ с^-1 — характерная частота оптических фононов, см. рис. 4.3). Такое предположение оправдано для оптических ветвей действительно слабой зависимостью  (см. рис. 4.3). Итак, в модели Эйнштейна (рис. 4.3)

                                      (4.21)

Свободная энергия для оптических фононов тогда равна

                       (4.22)

Внутренняя энергия

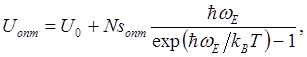                                        (4.23)

где предположено, что для всех оптических ветвей .

Учет вклада в промежуточной области температур акустических фононов в теплоемкость часто проводят в модели Дебая. В этой модели предполагается, что во всей области частот плотность состояний фононов имеет вид . Это выражение, правильно описывает функцию  лишь в области частот << . Поэтому интегрирование по частотам в модели Дебая должно быть ограничено характерной максимальной частотой . Ее появление связано с учетом конечного числа степеней свободы при колебаниях кристалла. Поскольку имеет всего 3N степеней свободы (для акустических ветвей, как мы видели, s= 1), то спектр должен обрываться на некоторой предельной частоте, в качестве которой берут . Эта частота  может быть найдена из условия нормировки функции :  

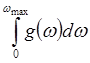                               =  3N                                                     (4.24)

Исходя из (4.24) и используя (4.12), получаем

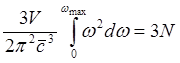                                        (4.25)

откуда

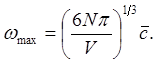                                           (4.26)

Заменяя в (4.25)  через по соотношению (4.26), получаем

С учетом этого обстоятельства, свободная энергия акустических фононов тогда имеет вид

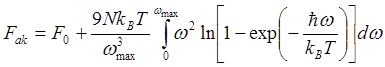               (4.27)

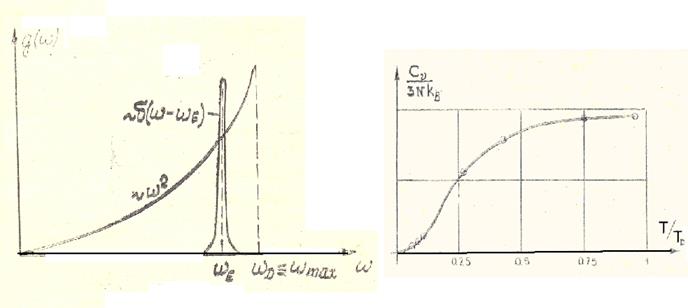
Рис.4.3                                      Рис.4.4

4.3. Теплоемкость кристаллической решетки

Внутренняя энергия фононов и их теплоемкость определяются по формулам:

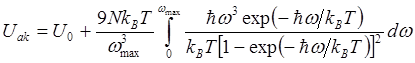                  (4.28)

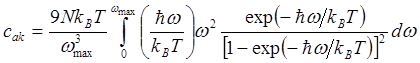          (4.29)

Введем температуру Дебая (где называется частотой Дебая). Тогда (4.28) и (4.29) принимают вид

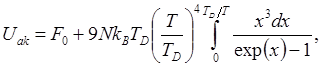                                             (4.30)

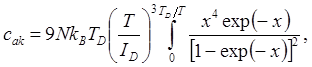                                           (4.31)

где .

Для расчета термодинамических характеристик кристаллов во всем диапазоне температур введем две функций D_E(T) и D_C(T), зависящие от характеристик кристалла и его температуры. D_E(T) носит название функция энергии Дебая и определяется так

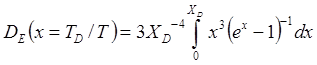.                                (4.32)

Функция D_C(T) называется функций теплоемкости Дебая.

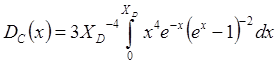.                                   (4.33)

Эти функции затаблированы в [?]. В (4.32), (4.33) ведены безразмерные параметры , – температура Дебая.

Для типичных решеток (например, для Аl ; для NaCl ; для К , но для С (алмаз) —). Из соотношения (2.70) видно, что теплоемкость является универсальной функцией . Таким образом, в дебаевском приближении весь спектр акустических фононов (очень сложная функция для реальных кристаллов) заменяется одним параметром — температурой Дебая .

Теперь внутренняя энергия (4.28) и теплоемкость кристалла (4.29) принимают вид

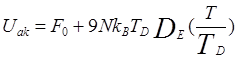                                             (4.34)

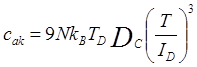 .                                          (4.35)